"数学，这门深奥而美妙的学科，总是让人不禁为之着迷。" 我们都曾学过自然数集，从1到无穷大，它们构成了我们理解世界的基础。然而，你是否想过，存在与自然数集对等的集合呢？

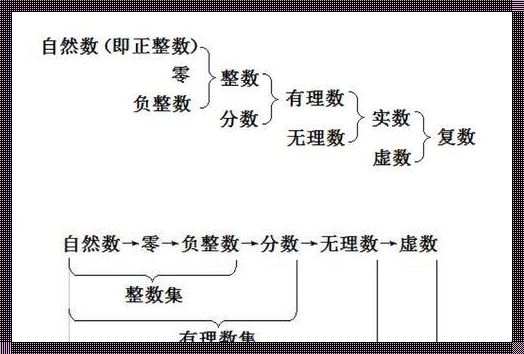
这个概念最初出现在我面前时，我也感到困惑。然而，经过深入思考和研究，我逐渐领悟到了它的美妙之处。这个与自然数集对等的集合，其实就是我们熟知的实数集。

实数集包含了所有的有理数和无理数，它们可以完美地映射到自然数集上。每一个自然数，都可以找到一个唯一的实数与之对应。反之亦然，每一个实数，都可以表示为自然数的某种组合。这就是与自然数集对等的集合的奇妙之处。

举个例子，让我们看看数字π。π是一个无理数，它不能用自然数来精确表示。然而，我们可以用自然数的无限序列来逼近π。例如，π的前三位是3.14，这可以表示为3+0.1+0.04。这里的3是自然数，而0.1和0.04可以用自然数的比例来表示。这就说明了π与自然数集的对等性。

这种对等性不仅仅存在于数学中，我们的日常生活中也充满了类似的例子。我们每个人都是独一无二的，但我们在社会中扮演的角色，比如学生、工作者、父母，都可以用自然数的集合来表示。每个人都是这个集合中的一个独特的元素，而我们的经历和身份，就是这些元素的组合。

这种对等性给了我们一种新的视角，去看待世界和自己的生活。我们不再仅仅是一个个孤立的个体，而是构成了一个庞大而有序的集合。这种观念让我感到无比震撼，也让我更加深入地理解了数学的魅力。

总的来说，与自然数集对等的集合，这个概念虽然抽象，但它揭示了数学中的一种美妙的对称性。它让我们看到了数学的深奥和美妙，也让我们对自己的生活和世界有了新的认识。