分布函数是概率论中的一个重要概念，它能够完整地描述一个随机变量的概率性质。在实际应用中，常用的分布函数有均匀分布、正态分布、指数分布等。

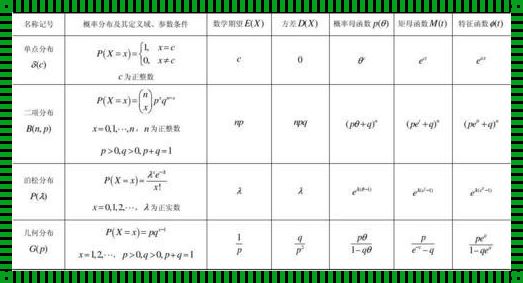
均匀分布是最简单的连续分布之一，它的分布函数为：

(a + b - x) / (b - a), 当 a < x < b 1, 当 x ≤ a 或 x ≥ b }

其中，a 和 b 分别为分布的上下限。

正态分布是自然界和社会科学中最为常见的分布之一，它的分布函数为：

F(x) = (1 / (σ√(2π))) * e^(-(x - μ)^2 / (2σ^2))

其中，μ 为分布的均值，σ 为分布的标准差。

指数分布是描述寿命或等待时间的常用分布，它的分布函数为：

F(x) = 1 - e^(-λx)

其中，λ 为分布的参数，表示单位时间内事件发生的平均次数。

这些分布函数在统计学、工程学、经济学等领域有着广泛的应用。例如，在工程领域，正态分布广泛应用于质量控制和可靠性工程；在经济学中，指数分布常用来描述投资收益的分布。

通过对这些分布函数的理解和应用，我们可以更好地分析和解决实际问题。例如，通过对产品寿命的指数分布进行分析，可以确定产品的维修策略和更换周期；通过对金融市场的正态分布进行研究，可以制定更为合理的投资策略。

总之，掌握常用的分布函数公式，不仅有助于我们更好地理解和描述客观世界的规律，还可以为我们的生产和生活带来实际的便利。