正四面体，一个简单而又神秘的几何图形，自古以来就吸引着无数数学家和几何学家的目光。它的独特性质和优美比例，使其在数学领域占有重要地位。而正四面体的棱切球半径公式，更是几何学中的一项重要成果。

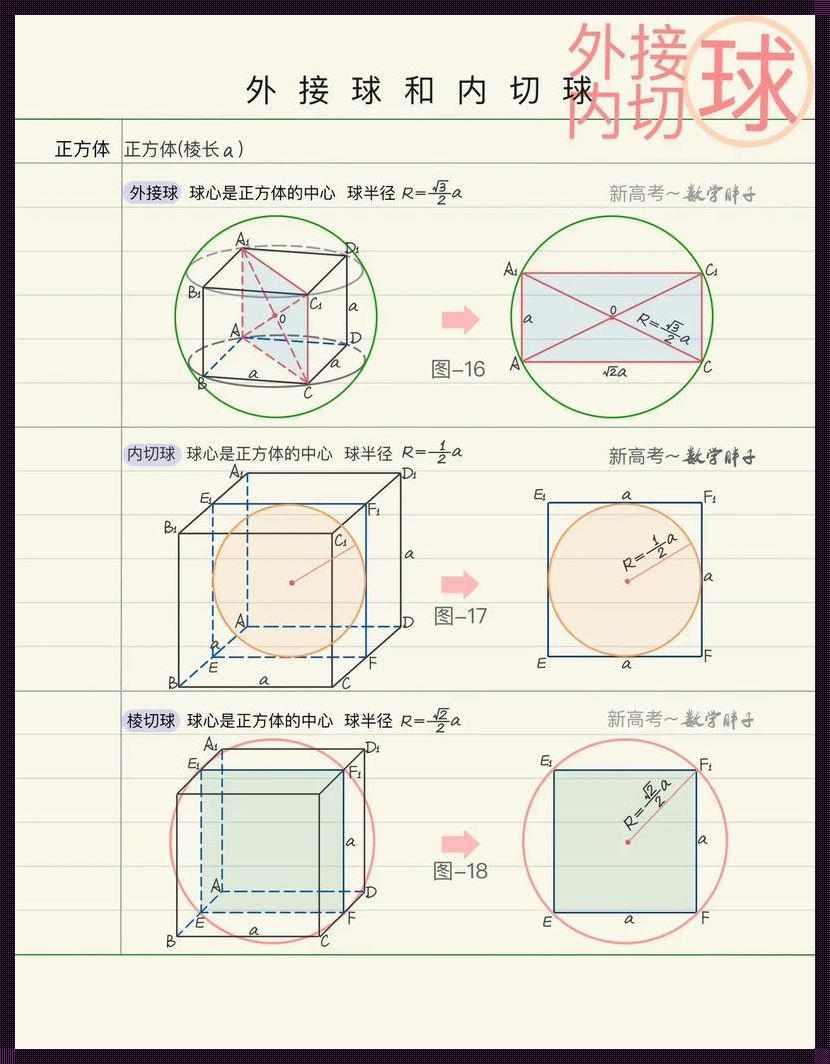
所谓正四面体的棱切球，是指正四面体的每个面都与球相切，且球的半径等于棱长。正四面体棱切球半径公式，就是用来计算这个球的半径的公式。

让我们先来简单介绍一下正四面体。正四面体，又称正四面体，是由四个等边三角形构成的多面体。它的每个面都是等边三角形，每个角都是109.5度。正四面体的棱长和棱切球的半径之间的关系，可以通过以下公式来表示：

其中，( R ) 表示棱切球的半径，( a ) 表示正四面体的棱长。

这个公式是如何得出的呢？我们可以通过以下步骤来进行推导：

首先，我们将正四面体切割成四个小的等边三角形。这样，原来的正四面体就被分割成了四个小的正四面体。由于每个小正四面体的棱长都等于原正四面体的棱长，因此，每个小正四面体的棱切球半径也等于原正四面体的棱切球半径。

接下来，我们考虑原正四面体的底面。底面是一个等边三角形，它的中心到每个顶点的距离都等于棱长。我们可以将底面中心到顶点的距离看作是棱切球的半径。

最后，我们可以发现，原正四面体的棱切球半径，等于连接底面中心和顶点的线段的一半。因此，我们得到了正四面体棱切球半径公式：

这个公式不仅简洁优美，而且揭示了正四面体与棱切球之间的内在联系。它使我们能够轻松计算正四面体的棱切球半径，从而更好地理解和应用正四面体的性质。

通过对正四面体棱切球半径公式的探究和解读，我们不仅加深了对几何图形的认识，也体会到了数学的奇妙和美丽。这个公式是我们几何学宝库中的一个重要成果，值得我们深入研究和传承。