"统计学中，置信区间计算公式就像一盏指路灯，照亮了我们寻找数据真实性的道路。" 每当我提及这个概念，我的脑海中总会浮现出那些繁复的数学符号和公式，它们犹如一首首优美的乐章，弹奏出统计学的韵律。

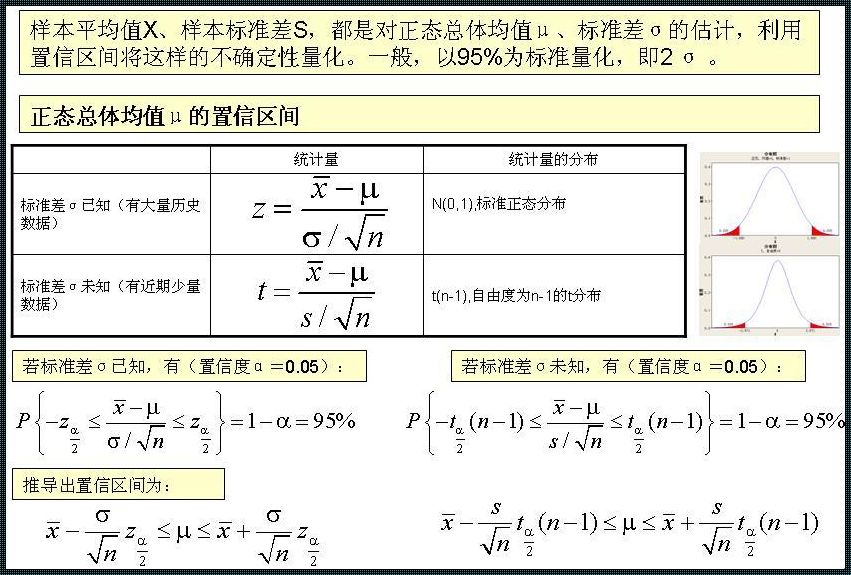
置信区间，简单来说，是对一个总体参数（如平均值、比例等）的估计范围。这个范围给出了我们相信总体参数真实值落在该区间内的概率。例如，我们可能会说，一个特定药物对疾病的治愈率为80%，其置信区间为（75%，85%）。这意味着，如果我们多次随机抽取样本并进行调查，那么大约80%的置信区间将包含真实治愈率。

那么，如何计算置信区间呢？这里有一个基本的原则：样本统计量加上或减去相应的抽样误差。抽样误差是由样本大小和总体标准差决定的。具体来说，我们有以下公式：

置信区间 = 样本统计量 ± Z * 抽样误差

这里的Z值取决于置信水平，通俗地讲，就是我们对总体参数的信心程度。例如，如果置信水平是95%，那么Z值通常是1.96（这是由标准正态分布表提供的）。

"想象一下，置信区间就像是我们对未知世界的一次探险。" 当我们使用这个公式，就像是给我们的估计值加上了一个范围，这个范围告诉我们可能出现的最坏情况和最好情况。这样，我们就可以更加准确地评估我们的估计，而不至于过于武断或过于保守。

然而，置信区间并非万能。它依赖于样本的随机性和抽样方法。如果样本不具有代表性，或者抽样方法存在偏差，那么置信区间可能会误导我们。因此，在实际应用中，我们需要结合具体情况，审慎地使用置信区间。

"置信区间计算公式，是我探索统计学世界的有力工具。" 每当我使用它，我都能感受到统计学的魅力和实用性。它不仅帮助我更好地理解数据，还让我在面对未知时，有了更强的信心和把握。

总结起来，置信区间计算公式是统计学中的一项重要工具，它为我们提供了估计总体参数真实值的范围。通过理解和应用这个公式，我们可以更加准确地评估数据，更加自信地面对未知。