方差是统计学中一个非常重要的概念，它用于衡量一组数据的离散程度。在实际应用中，我们常常需要寻找与方差相对应的统计量，以便更好地理解和分析数据。

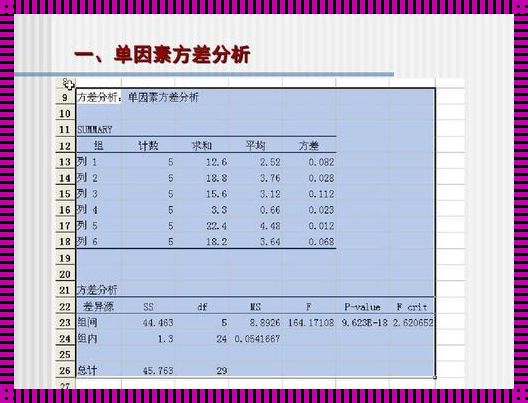
首先，我们需要明确一点，方差本身就是一个统计量，它衡量的是数据分布的离散程度。然而，在某些情况下，我们需要寻找与方差相对应的统计量，以便在不同场景下进行数据分析和处理。

与方差相对应的统计量有很多，其中一些常见的包括：

1. 标准差：标准差是方差的平方根，它也是一个非常重要的统计量。标准差越大，数据的离散程度就越大；反之，标准差越小，数据的离散程度就越小。

2. 变异系数：变异系数是标准差与平均值的比值，用于衡量数据的相对离散程度。变异系数越大，数据的相对离散程度就越大；反之，变异系数越小，数据的相对离散程度就越小。

3. 四分位数：四分位数是将数据分为四等份的数值，用于描述数据的分布情况。四分位数可以帮助我们了解数据的中间值和离散程度。

4. 偏度和峰度：偏度是衡量数据分布不对称程度的统计量，峰度是衡量数据分布峰态程度的统计量。偏度和峰度的值分别为0表示数据分布对称，大于0表示数据分布右偏，小于0表示数据分布左偏；峰度大于0表示数据分布有尖峰，小于0表示数据分布平坦。

这些与方差相对应的统计量可以帮助我们更全面地了解数据的分布特征，从而为实际应用提供更有力的支持。在实际数据分析过程中，我们需要根据具体情况选择合适的统计量，以便更好地解决问题。

总之，方差是统计学中一个非常重要的概念，与方差相对应的统计量可以帮助我们更全面地了解数据的分布特征。在实际应用中，我们需要根据具体情况选择合适的统计量，以便更好地解决问题。通过深入研究这些统计量，我们可以更好地应用统计学知识，为解决实际问题提供有力支持。