正四棱锥，这样一个简单的几何图形，却蕴含着无尽的奥秘。今天，让我们一起揭开它外接球半径公式的神秘面纱，感受几何之美。

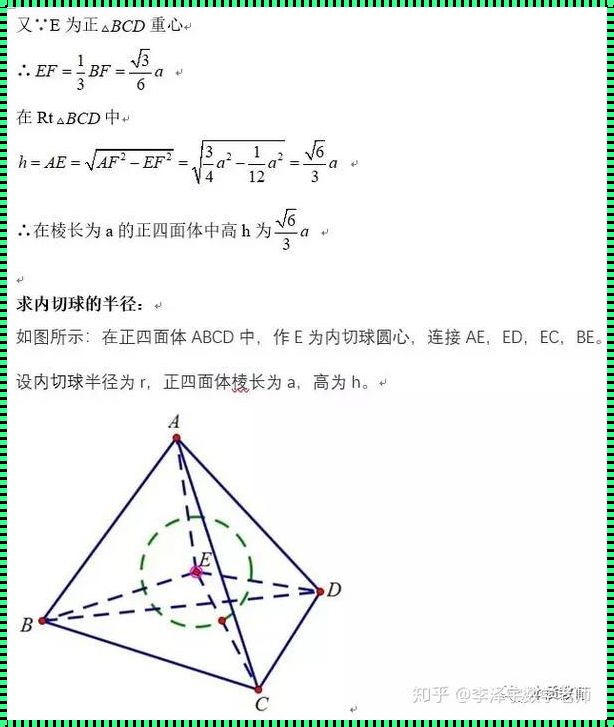
首先，让我们来了解一下正四棱锥的基本概念。正四棱锥是一个底面为正方形，顶点在底面正中央的四面体。它的侧面是四个等腰三角形，底面是一个正方形。

接下来，我们来探讨正四棱锥的外接球半径公式。所谓外接球半径，就是正四棱锥的顶点到其外接球心的距离。这个距离，可以用以下公式表示：

其中，正四棱锥的斜高，指的是从顶点到底面任一边的距离。

那么，如何推导出这个公式呢？这里，我们可以运用一些巧妙的方法。

首先，我们可以将正四棱锥切割成四个小的四面体。这四个小的四面体，都是相似的，且它们的底面分别是正四棱锥的四个侧面。由于相似性质，这四个小的四面体的外接球半径，与正四棱锥的外接球半径相等。

接着，我们来计算这四个小的四面体的外接球半径。我们可以将每个小的四面体看作是一个正四面体，其外接球半径已知。然后，通过一些几何变换，我们可以将正四棱锥的斜高转化为正四面体的边长。这样，我们就可以用正四面体的外接球半径公式，来计算出正四棱锥的外接球半径。

在这个过程中，我们会发现，正四棱锥的性质与正四面体有许多相似之处。正是这种相似性，让我们能够巧妙地运用正四面体的公式，来求解正四棱锥的问题。

通过这个公式的推导，我们不仅学会了如何求解正四棱锥的外接球半径，更重要的是，我们学会了如何运用相似性质，来解决几何问题。这种方法，不仅简洁高效，而且充满了美感。它让我们感受到，几何之美，不仅在于形状，更在于其内在的规律和联系。

总之，正四棱锥的外接球半径公式，是我们探索几何世界的一把钥匙。它让我们看到了几何的奥秘，也让我们体验到了发现的乐趣。希望这篇文章，能够帮助你更好地理解这个公式，也能够在几何的世界中，找到属于你的乐趣。