主成分分析法（Principal Component Analysis，PCA）是一种常用的多维数据分析方法，通过对数据进行线性变换，将原始数据映射到新的坐标系中，从而实现数据的降维。本文将通过简单的例题，揭秘主成分分析法的原理和应用。

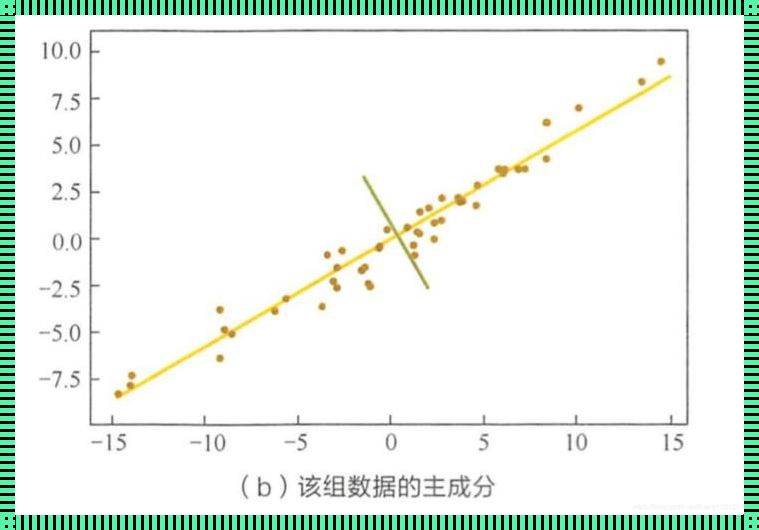
例题：假设我们有一组数据，表示某班级学生的身高和体重。我们希望通过主成分分析法，将这组数据降维，以便更好地进行数据分析和可视化。

首先，我们需要将数据进行标准化处理，使得每个特征的数值都在同一个数量级上。然后，我们计算数据的协方差矩阵，表示不同特征之间的相关性。接下来，我们求解协方差矩阵的特征值和特征向量。特征值表示新特征的重要性，特征向量表示新特征的方向。

根据特征值的大小，我们可以选择前几个最大的特征值对应的特征向量作为主成分。这些主成分能够解释大部分的数据 variance，即包含了原始数据的主要信息。最后，我们将原始数据投影到这些主成分上，得到降维后的数据。

通过这个例题，我们可以看到主成分分析法的作用是通过对数据进行降维，使得数据更容易进行分析和可视化。同时，主成分分析法也能够帮助我们发现数据中的隐藏结构和模式，从而更好地理解数据。

主成分分析法在实际应用中非常广泛，例如在图像处理、机器学习、数据挖掘等领域。通过使用主成分分析法，我们可以将高维数据转化为低维数据，从而简化了问题的复杂性，提高了计算的效率。同时，主成分分析法也能够帮助我们去除数据中的噪声和冗余信息，提高数据的质量。

总之，主成分分析法是一种强大的多维数据分析方法，通过降维，我们可以更好地理解和挖掘数据中的价值。希望通过这个简单的例题，能够让你对主成分分析法有一个更深入的认识。