当我们步入统计学的殿堂，假设检验是其中一门不可或缺的学问。它如同探索真理的灯塔，指引我们判断样本数据是否能够支持或者反对某个假设。在假设检验的世界里，z分布表是一个重要的工具，它为我们的推断提供了坚实的数学基础。

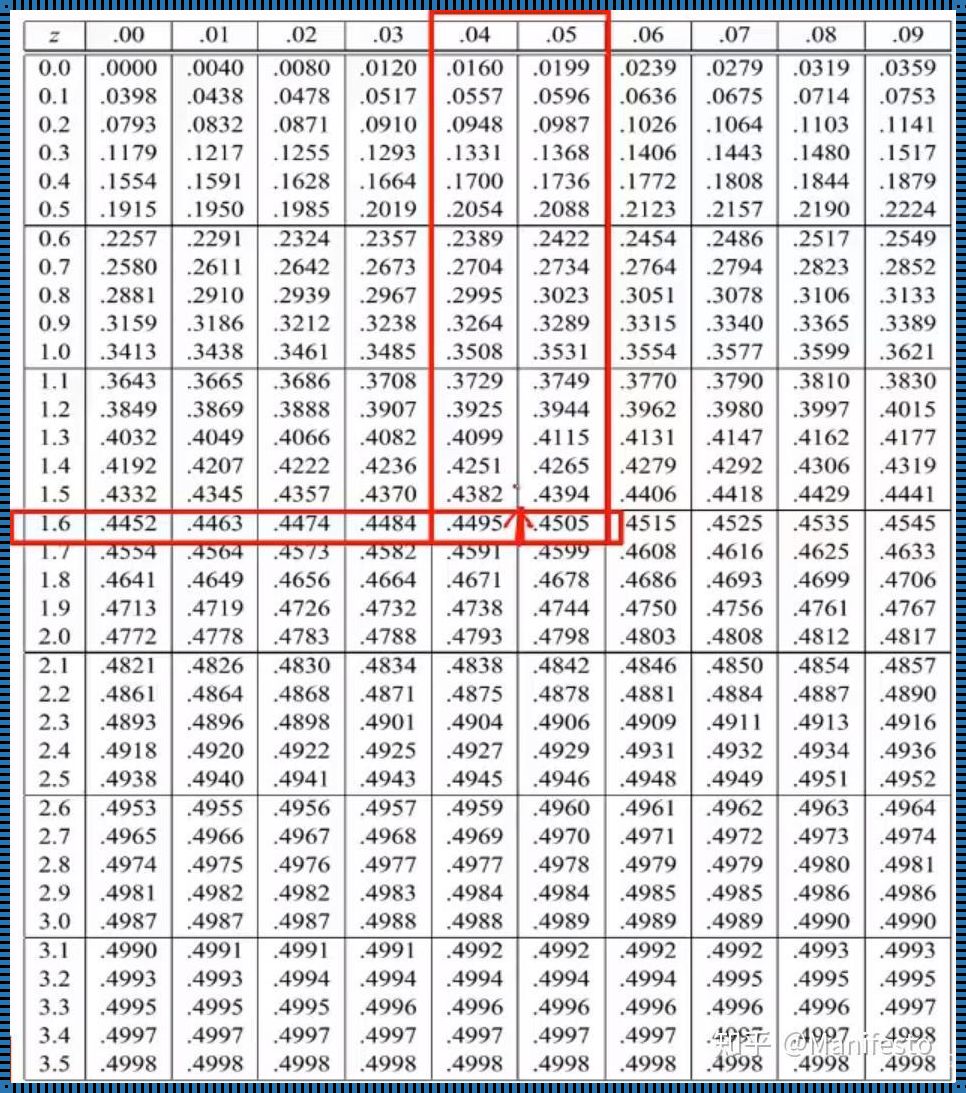
z分布，这个名字听起来就让人联想到它与空间的概念有着密切的联系。确实，在假设检验中，z分布就是将样本统计量映射到标准正态分布上的一种方法。这种映射，就如同我们在空间中确定一个点的位置，通过坐标轴上的数值来描述。当我们说一个样本统计量服从z分布时，实际上是在说这个统计量在标准正态分布上的位置已经确定，其对应的概率也随之明确。

在假设检验中，我们经常使用z分布表来查找临界值。这个临界值是我们的判断标准，它决定了我们是否拒绝原假设。当我们计算出的统计量值小于临界值时，我们倾向于接受原假设；反之，则倾向于拒绝。这个过程中，z分布表就是我们的指南针，帮助我们准确判断。

z分布表的应用空间广泛，无论是在医学研究、工程领域，还是在经济学、心理学等学科中，它都扮演着重要的角色。例如，在医学研究中，我们可能需要判断某种药物的治疗效果是否显著，这时就需要用到假设检验。通过计算样本统计量并查z分布表得到临界值，我们可以得出药物是否有效的结论。这样的应用，不仅关系到病人的健康，还可能影响到整个医疗行业的发展。

z分布表的空间理解，还涉及到它的性质。它是一种对称分布，这意味着正态分布的两边概率是相等的。此外，z分布还具有单峰性，即所有的数据都集中在分布的峰值附近。这些性质使得z分布在假设检验中具有极高的实用价值。

然而，z分布表并非万能。在实际应用中，我们还需要考虑样本量的大小。当样本量较小的时候，z分布就可能不再适用，此时我们需要转向t分布。t分布与z分布类似，但它更加灵活，能够适应小样本量的需求。

总的来说，z分布表在假设检验中的应用，就如同在广阔的空间中为我们点亮了一盏明灯。它帮助我们在数据的海洋中找到方向，做出科学的判断。理解和运用z分布表，不仅能够加深我们对统计学知识的理解，还能够提高我们的数据分析能力，让我们在探索未知的世界中更加自信和从容。