主成分分析法（PCA）是一种常用的数据分析技术，它可以帮助我们从高维数据中提取出最重要的信息，并在降低数据维度的同时保持数据的信息量。在这个过程中，PCA将数据转换为一个坐标系，使得数据点在这个坐标系中的分布能够尽可能地揭示数据的内在结构。

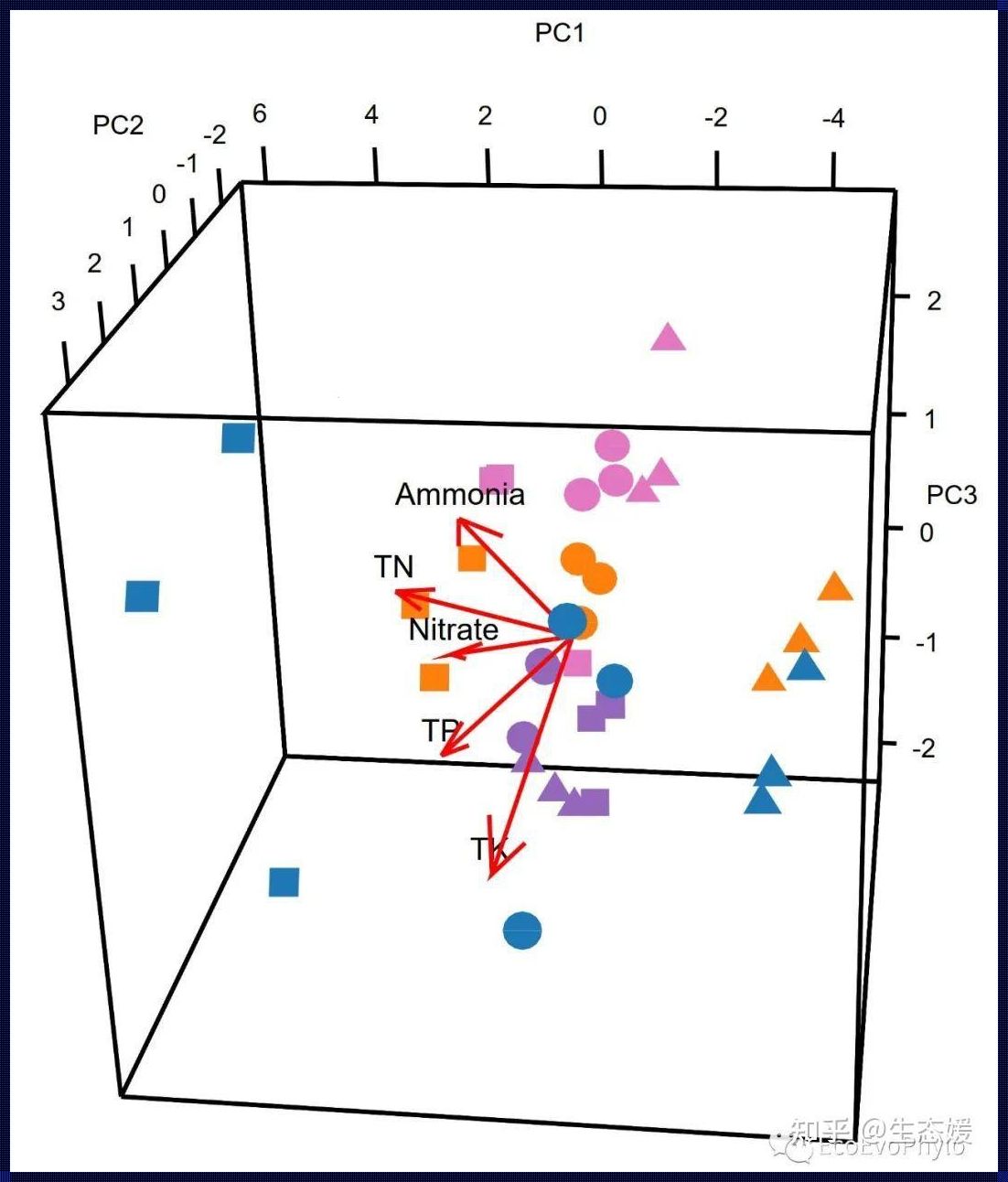
“数据是新时代的石油”，这句话道出了数据对于现代社会的重要性。然而，数据的数量和复杂性也在不断增加，这就需要我们运用先进的分析方法来挖掘数据的价值。这时，PCA就成为了一种不可或缺的工具。

举个例子，假设我们有一组关于人的身高、体重、年龄和收入的数据，我们希望通过这些数据来探究它们之间的关系。然而，这些变量之间可能存在多重共线性，这就使得我们很难从中找到真正的规律。这时，我们可以使用PCA来降维，将这四个变量转化为两个或三个主成分，这样我们就可以在降低数据维度的同时保留数据的主要信息。通过这两个或三个主成分，我们可能就会发现身高、体重和年龄之间存在着某种关系，而收入则可能是这种关系的调节变量。

PCA的应用不仅仅局限于统计学领域，它已经广泛应用于机器学习、图像处理、语音识别等多个领域。例如，在机器学习中的分类任务中，我们可以使用PCA来降低数据的维度，从而提高模型的训练速度和准确率。在图像处理中，PCA可以帮助我们提取图像的主要特征，从而实现图像的压缩和识别。

然而，尽管PCA有着广泛的应用，但我们也不能盲目地使用它。PCA的效果很大程度上取决于数据的质量和特征选择。在实际应用中，我们需要根据具体问题来选择合适的PCA参数，并通过交叉验证等方法来评估模型的性能。

总的来说，主成分分析法PCA是一种强大的数据分析工具，它可以帮助我们从复杂的数据中揭示出背后的规律和关系。然而，要想充分发挥PCA的优势，我们需要对数据有深入的理解，并运用适当的技巧来优化PCA的参数。通过这种方式，我们可以将PCA应用于各种领域，从而为解决实际问题提供有力的支持。