向量，作为数学领域的基础概念，其重要性不言而喻。而向量的行秩，则是向量空间中的一个重要性质。本文将从向量的行秩的定义、意义以及防范和应用等方面，对其进行深入探讨。

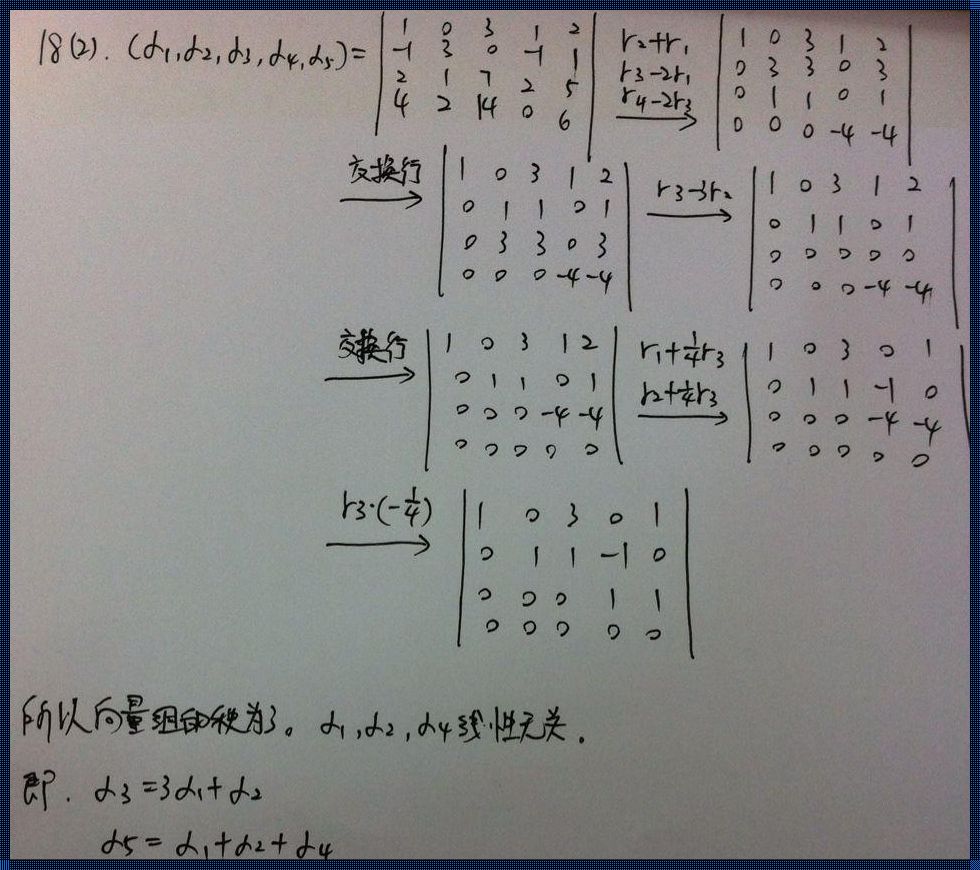
首先，什么是向量的行秩？行秩，又称秩，是一个线性变换或矩阵的列空间（或行空间）的维数。换句话说，就是一个矩阵中线性无关的行（或列）的最大数目。这个概念在线性代数中起着非常重要的作用，比如在解决线性方程组、研究矩阵性质等问题时，都需要涉及到行秩。

那么，如何防范行秩的问题呢？其实，防范行秩的问题，主要就是要避免线性相关性的出现。在实际应用中，我们可以通过以下几种方法来实现：

1. 选定基底：在研究向量空间时，首先需要选定一个基底。一个好的基底可以使得向量空间的结构更加清晰，便于我们研究其中的向量。

2. 线性组合：对于一组向量，我们可以通过线性组合的方式来构造新的向量。在这个过程中，我们需要注意避免产生线性相关的向量。

3. 矩阵的秩：在处理矩阵时，我们可以通过计算矩阵的秩来判断其列向量（或行向量）是否线性相关。如果矩阵的秩小于其行数（或列数），则说明矩阵中存在线性相关的行（或列）。

接下来，我们来看一下向量的行秩的应用。行秩在实际生活中有着广泛的应用，例如：

1. 图像处理：在图像处理中，行秩可以用来判断图像的维度，从而进行图像的压缩和恢复。

2. 数据挖掘：在数据挖掘中，行秩可以用来分析数据的线性结构，从而提取有效的信息。

3. 物理学：在物理学中，行秩可以用来研究物理系统的状态空间，从而分析系统的稳定性和演化过程。

总之，向量的行秩是一个非常重要的概念，它在数学、计算机科学、物理学等领域都有着广泛的应用。我们应该充分理解其定义和性质，掌握其防范和应用的方法，以便更好地解决实际问题。