在向量空间中，两个向量的点积（内积）运算被广泛应用于数学、物理、工程等多个领域。向量a与向量b的点积，通常表示为a·b，不仅仅是一个数值，它还携带了两个向量之间的重要信息。

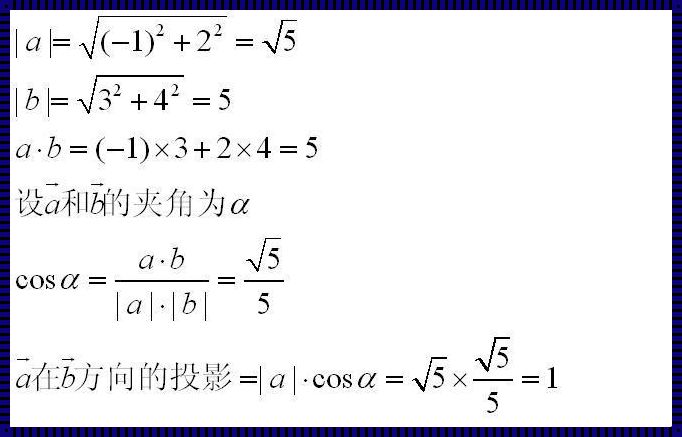
想象在二维空间中，有一个向量a，它从原点指向一个点(x1, y1)，另一个向量b指向点(x2, y2)。那么，向量a与向量b的点积可以被理解为从原点到点(x1, y1)的“投影”与从原点到点(x2, y2)的“投影”之间的“夹角余弦”的乘积乘以两点之间的距离。数学表达式为：

[ a \cdot b = |a| |b| \cos(\theta) = x1x2 + y1y2 ]

这里的( |a| )和( |b| )分别是向量a和向量b的长度（模），而( \theta )是向量a和向量b之间的夹角。

当我们深入探讨向量a·b的物理意义时，我们可以将其理解为向量a对向量b的“作用力”，在特定方向上的“效应”。比如，在物理学中，两个力向量的点积等于这两个力的“合力”在它们“夹角”方向上的分量，并且与这两个力的“夹角”余弦值成正比。

此外，在编程和计算机图形学中，向量的点积经常用于计算旋转矩阵，以确定物体在空间中的旋转。而在信号处理领域，两个信号向量的点积可以解释为它们的“相关性”，这在统计学和模式识别中有着重要应用。

然而，要真正掌握向量的点积，除了理论学习之外，还需要通过大量的实践和应用。它可以简化复杂问题，提供直观的视角，帮助我们理解事物之间的内在联系。

分享这一知识，不仅是传递一个数学概念那么简单，更是在传递一种思考问题、解决问题的方法。它激励我们探索未知，挑战自我，用科学的视角去观察和理解这个世界。

如同英国著名数学家希尔伯特所说：“数学是自由的女神，她从不绑定于任何特定的国家或时代。”让我们以向量的点积为例，继续在知识的海洋中遨游，探寻那些隐藏在简洁公式背后的深邃意义。