"世间万物，皆有规律。" 这句话对于几何学来说，再合适不过了。今天，让我们一起探索棱柱内切球半径的万能公式，解析其中蕴含的奥秘。

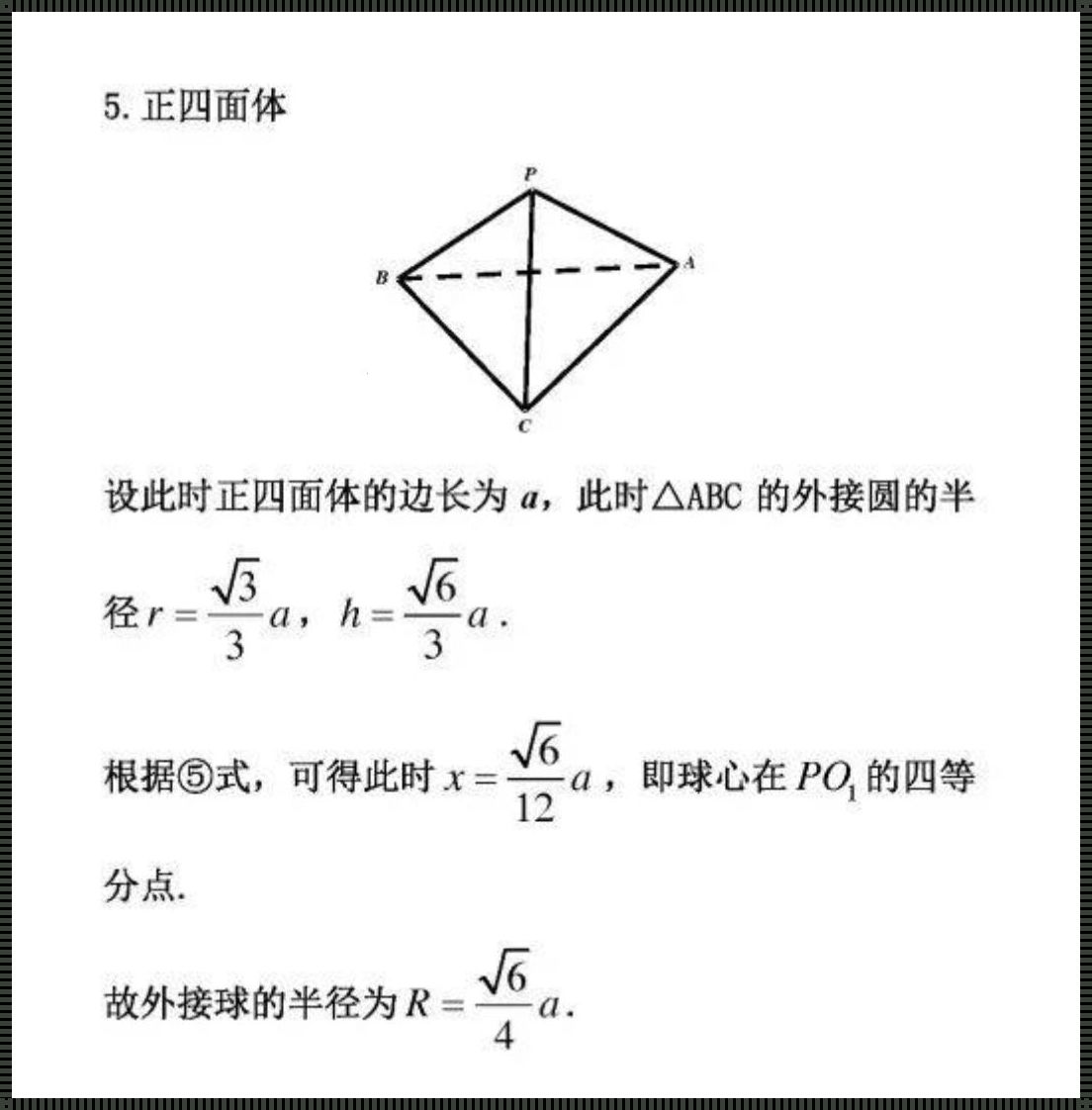
棱柱，这个我们在中学时期就熟悉的几何图形，由上下两个平行且相等的多边形底面和连接这两个底面的矩形侧面组成。而内切球，则是这个棱柱内部的一个球，它的球心位于棱柱的中心，并且球面与棱柱的各个面都相切。

那么，如何求解棱柱内切球的半径呢？这就需要引入一个重要的概念——棱柱的轴截面。轴截面是棱柱的一个平行于底面的横截面，它将棱柱分成两个对称的部分。棱柱内切球的半径，就是这个轴截面内切圆的半径。

让我们以直棱柱为例，来推导这个公式。假设直棱柱的底面是一个n边形，边长为a，高为h，内切球的半径为r。那么，我们可以发现，内切球在轴截面上的投影，恰好是轴截面内切圆的圆心。根据勾股定理，我们可以得到以下关系式：

这个公式就是直棱柱内切球半径的万能公式。它告诉我们，只要我们知道了一个直棱柱的底面边长和高，就可以求出它的内切球半径。

然而，世界上的事物并非总是那么简单。对于斜棱柱，情况就变得复杂了。斜棱柱的轴截面是一个非圆形的椭圆，这使得内切球的半径的求解变得困难。但是，通过对几何形状的深入研究和巧妙地运用代数方法，我们仍然可以得到斜棱柱内切球半径的公式。

总的来说，棱柱内切球半径的万能公式，不仅是对几何学规律的探索，更是对人类智慧的挑战。它让我们明白，只要有足够的耐心和智慧，就没有解不开的谜题。

希望这篇文章能激发你对几何学的兴趣，让我们一起在几何的世界里，探索无限的可能。