在三维空间中，法向量是一个非常重要的概念，它可以帮助我们更好地理解和描述空间中的几何形状和物体。那么，如何求解三维空间中的法向量呢？

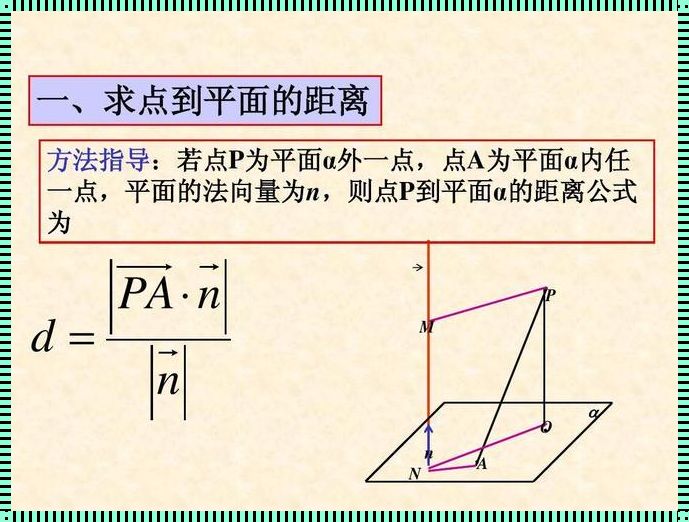
首先，我们需要明确法向量的定义。法向量是指与一个平面垂直的向量，它可以用来描述平面的方向和倾斜程度。在三维空间中，法向量通常表示为(a, b, c)，其中a、b、c分别是法向量在x、y、z轴上的分量。

求解三维空间中的法向量，一般可以通过以下几种方法：

1. 点法式：如果我们已知平面上的一个点和平面的法向量，那么可以通过点法式来求解平面的方程。点法式的一般形式为：ax + by + cz + d = 0，其中(a, b, c)是法向量，(x, y, z)是平面上的点的坐标，d是常数。

2. 叉乘：在三维空间中，两个向量的叉乘可以得到一个垂直于这两个向量的向量，这个向量就是我们要找的法向量。如果我们有两个向量A和B，它们的坐标分别为(Ax, Ay, Az)和(Bx, By, Bz)，那么它们的叉乘得到的法向量的坐标为：(AyBz - AzBy, AzBx - AxBz, AxBy - AyBx)。

3. 单位法向量：有时候我们需要的不是任意方向的法向量，而是单位法向量，即长度为1的法向量。这时候，我们可以通过将任意法向量除以其长度来得到单位法向量。

通过以上方法，我们就可以求解出三维空间中的法向量了。但是，需要注意的是，法向量的求解并不是一件简单的事情，它需要我们深入理解三维空间中的向量和几何知识，才能更好地应用和操作。

总之，三维空间中的法向量是一个非常重要的概念，它可以帮助我们更好地理解和描述三维空间中的几何形状和物体。通过点法式、叉乘和单位法向量等方法，我们可以求解出三维空间中的法向量，从而更好地理解和应用三维空间中的几何知识。