图论作为数学领域中一个重要的分支，一直以来都吸引着众多学者的关注。而在图论中，简单图同构的充要条件是一个核心问题，也是本文要探讨的主题。

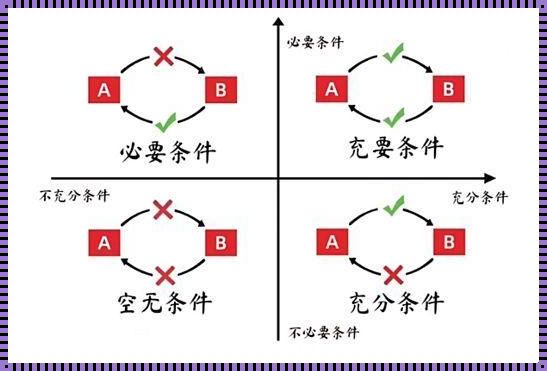
简单图同构，指的是两个简单图在结构上完全相同，即它们具有相同的顶点和边，并且相应的顶点和边完全对应。那么，什么条件下两个简单图才是同构的呢？

首先，我们需要了解简单图的定义。简单图是一种无向图，其中没有重复的边和顶点，并且图中没有环。这个定义为我们提供了一个基本的概念框架，以帮助我们探究简单图同构的充要条件。

在探究这个问题时，我们可以从顶点、边以及它们之间的关系入手。首先，两个简单图的顶点数必须相同。这是因为，如果两个图的顶点数不同，那么它们在结构上必然不同，从而不可能是同构的。

其次，两个简单图的边数也必须相同。这是因为，如果两个图的边数不同，那么它们在结构上必然不同，从而不可能是同构的。

最后，两个简单图的顶点和边之间必须满足一定的对应关系。具体来说，对于两个简单图G1和G2，如果它们是同构的，那么存在一个一一对应的映射f：V(G1) → V(G2)，使得对于G1中的任意一条边(u,v)，在G2中都存在一条与之对应的边(f(u),f(v))。

综上所述，两个简单图同构的充要条件是：它们的顶点数相同，边数相同，并且顶点和边之间存在一一对应的映射，使得相应的顶点和边完全对应。

通过对简单图同构的充要条件的探究，我们不仅加深了对图论的理解，也体会到了数学世界的奥秘。希望这篇文章能够激发大家对图论的兴趣，进一步探索图论的更多精彩内容。