排序算法是计算机科学中最为基础和常用的算法之一。在日常生活和工作中，我们经常会遇到需要对一系列数据进行排序的情况。而排序算法正是解决这一问题的有效手段。

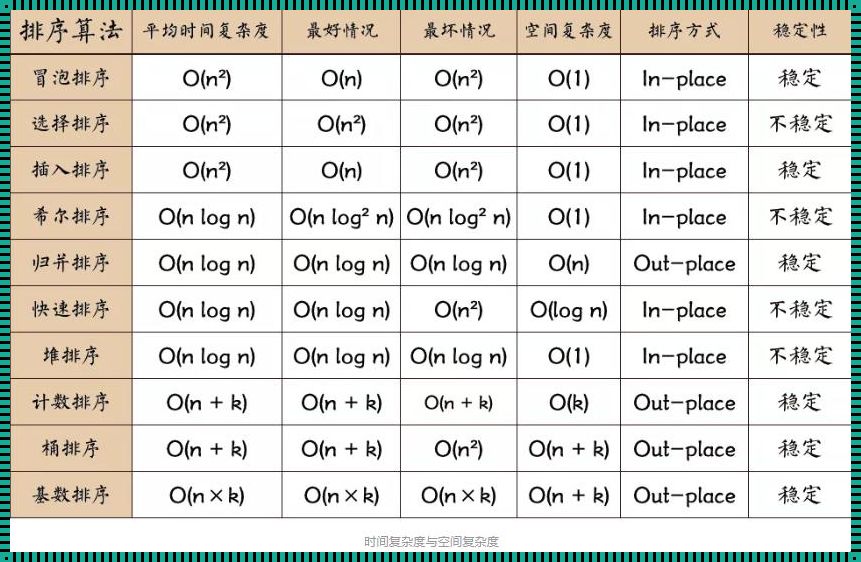
在众多的排序算法中，十大排序算法无疑是其中最为重要的。它们分别是冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序、希尔排序、计数排序、基数排序和桶排序。

那么，这些排序算法的时间复杂度又是如何的呢？

冒泡排序的时间复杂度为O(n^2)，它通过不断地比较和交换相邻元素的位置，使得最大的元素逐渐移动到数组的末尾。选择排序的时间复杂度同样为O(n^2)，它通过每次选择剩余元素中的最小（或最大）元素，然后放入已排序部分的末尾。插入排序的时间复杂度为O(n^2)，它通过将未排序部分的元素插入到已排序部分的合适位置，从而完成排序。

快速排序的时间复杂度为O(nlogn)，它通过选择一个基准元素，将数组分为两个子数组，然后递归地对这两个子数组进行排序。归并排序的时间复杂度同样为O(nlogn)，它通过将数组分成若干个子数组，然后将这些子数组合并为有序的数组。堆排序的时间复杂度为O(nlogn)，它通过构建堆，然后不断将堆顶元素与堆底元素交换，从而完成排序。

希尔排序的时间复杂度为O(nlogn)，它通过将数组分成若干个子数组，然后对每个子数组进行插入排序，随着子数组大小的逐渐减小，最终完成整个数组的排序。计数排序的时间复杂度为O(n+k)，其中k为数组中最大值的大小，它通过统计每个元素出现的次数，然后按照顺序输出。

基数排序的时间复杂度为O(nk)，其中k为数组中最大值的大小，它通过将数组按照每个位数进行分组，然后对每个位数进行排序。桶排序的时间复杂度为O(n+k)，其中k为桶的数量，它通过将数组中的元素分配到不同的桶中，然后对每个桶进行排序。

通过比较这些排序算法的时间复杂度，我们可以发现，快速排序、归并排序和堆排序的时间复杂度较为优秀，它们都能在较短的时间内完成排序。而冒泡排序、选择排序和插入排序的时间复杂度较高，它们在处理大量数据时会显得较为缓慢。

排序算法的选择和应用需要根据具体的问题和数据特点来进行。在实际应用中，我们需要根据数据规模、数据分布和性能要求等因素，选择合适的排序算法。同时，我们还可以通过优化和改进算法，提高排序的效率和性能。

总之，排序算法的时间复杂度是衡量算法性能的重要指标。通过对不同排序算法的时间复杂度进行分析和比较，我们可以更好地理解和掌握排序算法的原理和应用，从而在实际问题中做出更明智的选择和决策。