在统计分析的世界里，方差齐性是一个重要的假设。它指的是不同样本或群体的方差是否相等。当方差齐性不满足时，我们该怎么办？别急，我们一起去探索。

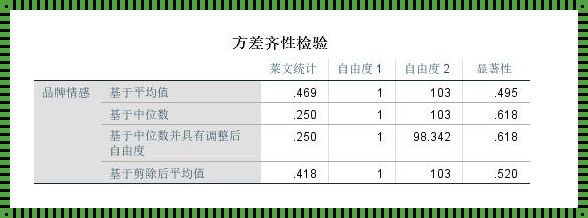
首先，我们要明白，方差齐性之所以重要，是因为它影响到我们对总体参数的估计和假设检验的结论。当方差不齐时，我们可能需要使用一些替代方法来进行检验。

替代方法之一是使用非参数检验。非参数检验不需要满足正态分布和方差齐性的假设，因此它是一种很实用的选择。例如，曼-惠特尼U检验（Mann-Whitney U test）就常用于比较两个独立样本的中位数是否相等，而威尔科克森符号秩检验（Wilcoxon signed-rank test）则用于比较两个相关样本的中位数。

另一种方法是对方差进行变换。例如，我们可以使用对数变换来使数据的方差趋于稳定。这种方法需要我们先对数据进行变换，然后再进行传统的参数检验。但是，这种方法需要我们对数据的变换方式有足够的了解，以避免产生误导性的结果。

此外，我们还可以使用贝叶斯统计方法。贝叶斯统计是一种基于概率的统计方法，它允许我们利用先验信息来进行推断。在方差齐性不满足的情况下，我们可以使用贝叶斯方法来估计总体参数，同时考虑到方差的不确定性。

总的来说，当方差齐性不满足时，我们有很多选择。我们可以使用非参数检验，对方差进行变换，或者使用贝叶斯统计方法。每种方法都有其优点和局限性，我们需要根据具体的问题和数据来选择最合适的方法。

记住，方差齐性不满足并不是世界末日，只要我们选择合适的方法，就能很好地解决这个问题。所以，别担心，一起加油吧！