矩阵，这个在数学、物理、工程等领域中广泛应用的概念，对于我们来说既熟悉又陌生。当我们谈论矩阵的秩时，实际上是在讨论矩阵中线性独立的行或列的最大数量。而当矩阵的第一列全为0时，我们该如何求其秩呢？

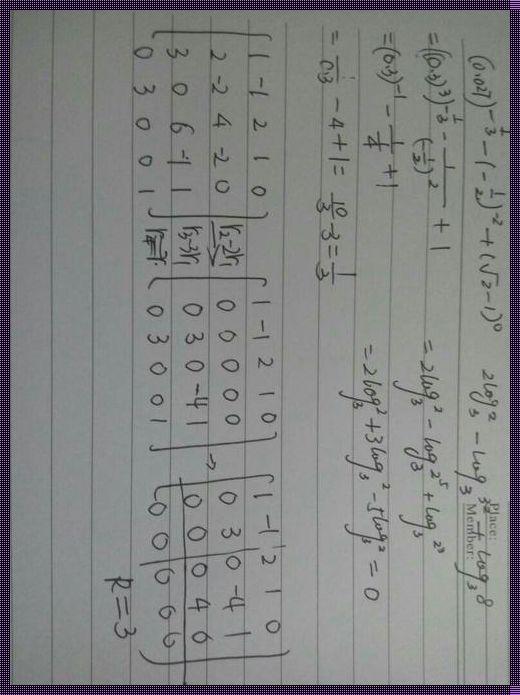
首先，我们需要明白，矩阵的秩是其最小非零子矩阵的行数或列数。也就是说，我们要找到一个非零的子矩阵，使得其行数或列数最小，这个最小数就是矩阵的秩。

那么，当矩阵的第一列全为0时，我们可以将其看作是一个二维零矩阵。在这种情况下，我们很难直接求出其秩，因为任何包含全零列的矩阵的秩都不会超过1。

然而，我们不能因此就断定这个矩阵的秩就是1。我们需要进一步分析矩阵的其他列，看看是否有可能存在线性独立的列。如果存在，那么这些列将构成矩阵的秩。

我们可以通过高斯消元法或者矩阵的秩运算性质来求解。首先，我们将矩阵的第一列去掉，然后对剩下的矩阵进行行变换，使其成为一个上三角矩阵。接着，我们可以通过计算上三角矩阵的行数来得到原矩阵的秩。

需要注意的是，如果矩阵的第一列全为0，那么我们在进行行变换时，要将第一列以外的其他列与第一列进行组合，以消除第一列全为0的影响。这样，我们才能得到一个正确的秩。

总之，当矩阵的第一列全为0时，我们不能直接求其秩，而需要通过分析矩阵的其他列来确定秩的大小。在这个过程中，我们可以运用高斯消元法或者矩阵的秩运算性质来求解。希望这篇文章能帮助你揭开矩阵第一列全为0求秩的神秘面纱。