在科技领域，数据分析是不可或缺的一环。而在数据分析中，方差计算公式是一个重要的统计工具，用于衡量一组数据的波动程度。本文将深入探讨方差计算公式的原理和应用，帮助你更好地理解数据背后的波动奥秘。

方差计算公式的基本原理

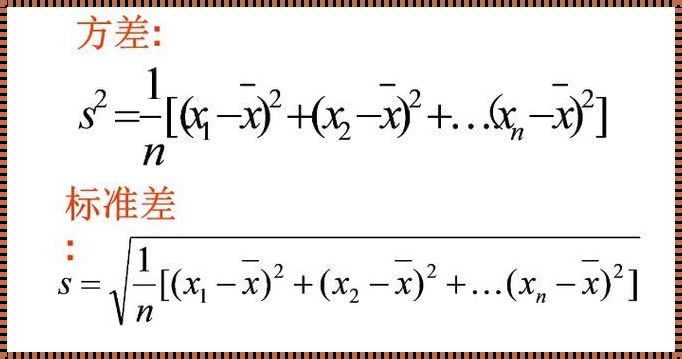
方差计算公式是用来衡量一组数据的离散程度的。具体来说，它表示的是各个数据点与平均值之间的差的平方的平均值。其数学表达式如下：

$$ $$

其中，$\sigma^2$ 表示方差，$n$ 表示数据点的个数，$x_i$ 表示第 $i$ 个数据点，$\mu$ 表示平均值。

方差计算公式的应用

方差计算公式在实际应用中有着广泛的应用。以下是一些常见的场景：

数据质量评估

在数据采集和处理过程中，通过计算数据的方差，可以评估数据的质量。方差较小的数据表示数据比较稳定，波动程度较小，而方差较大的数据则表示数据波动较大，可能存在异常值或噪声。

数据分析与挖掘

在数据分析与挖掘中，方差计算公式可以帮助我们了解数据的分布特征。通过计算不同特征的方差，可以对数据进行降维处理，提取出最重要的特征，从而简化数据分析和挖掘的过程。

机器学习与人工智能

在机器学习和人工智能领域，方差计算公式也有重要的应用。例如，在训练神经网络时，通过计算预测结果与真实值的方差，可以评估模型的准确性和稳定性。

总结

方差计算公式是科技领域中非常重要的统计工具，它可以帮助我们理解和分析数据背后的波动奥秘。通过掌握方差计算公式，我们可以更好地评估数据质量、进行数据分析和挖掘，以及评估机器学习模型的性能。

希望本文能够帮助你更深入地理解方差计算公式的原理和应用，让你在科技领域的探索之路更加顺利。