在几何的王国里，正四面体以其独特的对称性和简洁的构造，赢得了无数数学家和艺术家的青睐。它不仅仅是一个简单的三维形状，更是一个充满智慧和美学的几何体。今天，我们将探索正四面体的高与棱长之间的神秘关系，以及这种关系如何揭示了宇宙中和谐与秩序的奥秘。

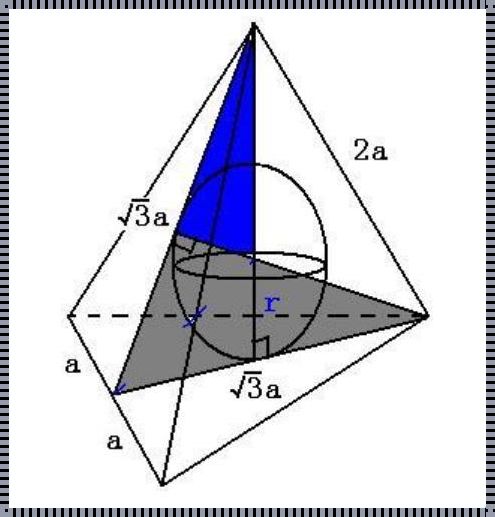
正四面体，由四个等边三角形面组成，每个顶点都与其他三个顶点相连，形成了一个完美的四面体结构。它的每一个面都是一个等边三角形，每一个顶点都等距离地连接着其他三个顶点。这种完美的对称性，不仅在视觉上给人以美的享受，更在数学上展示了一种深刻的内在联系。

当我们谈论正四面体的高，我们指的是从顶点垂直向下到对面中心的线段。这条高线，虽然在三维空间中只是一条简单的线段，但它却承载着正四面体内部结构的精髓。它将正四面体的顶点与底面紧密相连，形成了一个从顶点到中心的垂直通道。

棱长，作为正四面体的基本参数，决定了整个几何体的大小和比例。每一个棱的长度都是相等的，这种等长的特性，使得正四面体在数学上具有了独特的地位。棱长与高之间的关系，并非简单的线性关系，而是一种更为复杂的几何关系。

要计算正四面体的高，我们可以利用勾股定理和等边三角形的性质。假设正四面体的棱长为a，那么从顶点到底面的中心（即高的中点）的距离，可以通过以下公式计算得出：

这个公式揭示了正四面体的高与棱长之间的精确数学关系。它不仅展示了数学之美，更体现了自然法则中的和谐与平衡。高与棱长之间的关系，就像是一首精妙的交响乐，每一个音符都恰到好处，共同创造出一种完美的和谐。

在更深层次上，正四面体的高与棱长的关系，反映了宇宙中的基本规律。在自然界中，从分子结构到星系的排列，我们都能找到这种和谐与秩序。正四面体的这种特性，或许正是自然界中普遍存在的黄金比例的一个缩影。

正四面体的高与棱长之舞，是一种无声的语言，它诉说着几何的奥秘，数学的严谨，以及自然界的和谐。当我们深入探索这种关系时，我们不仅能够获得知识上的满足，更能够感受到一种超越物质世界的美和秩序。

随着时间的推移，正四面体的高与棱长之间的关系，将会继续激发着人们的好奇心和探索欲。它不仅是数学家研究的对象，也是艺术家创作的灵感来源。这种关系，将会像一篇永恒的诗篇，被后人传颂，成为人类文明中不可磨灭的一部分。