几何学是数学的一颗璀璨明珠，而正四棱锥则是几何学中一种独特的几何体。它既有四棱锥的稳定性，又具备正多边形的对称美。今天，就让我们一起来探索正四棱锥如何建立坐标系的奥秘。

一、正四棱锥的几何特性

正四棱锥是一种四棱锥，底面为正方形，侧面为四个全等的等腰三角形。它的底面对角线相等，且垂直于底面。我们若想为正四棱锥建立一个坐标系，就必须先了解这些基本的几何特性。

• 底面边长：正四棱锥的底面边长是建立坐标系的关键参数。
• 侧棱长：侧棱长是正四棱锥侧面的斜边长度，也是坐标系建立的重要依据。
• 高：正四棱锥的高将决定坐标系的垂直方向。

二、建立坐标系的方法

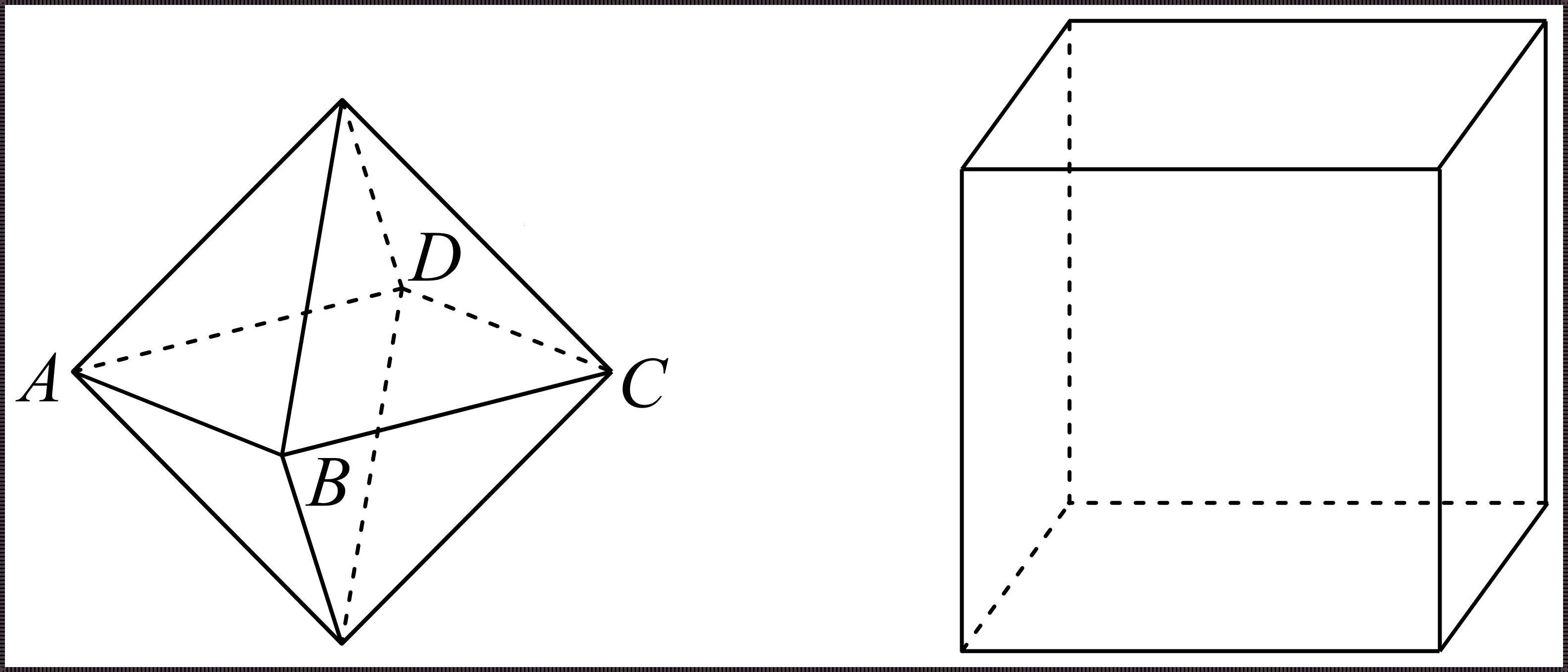
在了解正四棱锥的几何特性后，我们可以采用以下方法为其建立坐标系：

1. 确定底面坐标系：以正四棱锥底面的对角线为基准，建立二维直角坐标系。底面边长的一半作为坐标轴的长度。
2. 引入垂直坐标轴：在底面坐标系的基础上，沿着垂直于底面的方向引入第三个坐标轴，即高度坐标轴。
3. 确定顶点坐标：根据正四棱锥的侧棱长和高，可以计算出顶点的坐标。顶点坐标为（0, 0, h），其中h为正四棱锥的高度。

三、坐标系的实际应用

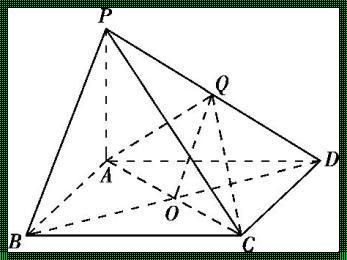
建立了正四棱锥的坐标系后，我们可以将其应用于以下几个方面：

• 计算体积：利用坐标系，可以轻松计算出正四棱锥的体积。
• 计算表面积：通过坐标系，可以计算出正四棱锥的底面积和侧面积，进而得到总表面积。
• 空间解析：坐标系有助于我们更好地理解正四棱锥在空间中的位置和运动。

四、结语

正四棱锥建系的方法不仅是对几何学的一种探索，更是对空间观念的一种深化。通过这篇文章，我们了解了正四棱锥的几何特性，学会了如何为其建立坐标系，并探讨了坐标系在实际应用中的价值。希望这篇文章能让你在几何学的道路上更进一步，感受到数学的神奇与美丽。

最后，让我们用一句话来总结：正四棱锥建系，奥秘无穷，探索无止境。