在几何学的世界里，异面直线所求角问题曾让无数英雄好汉竞折腰。今天，就让我们抛开繁琐的定理证明，换一个轻松愉悦的心情，探索这个主题的独特魅力，并为你揭秘一些解题的小技巧。

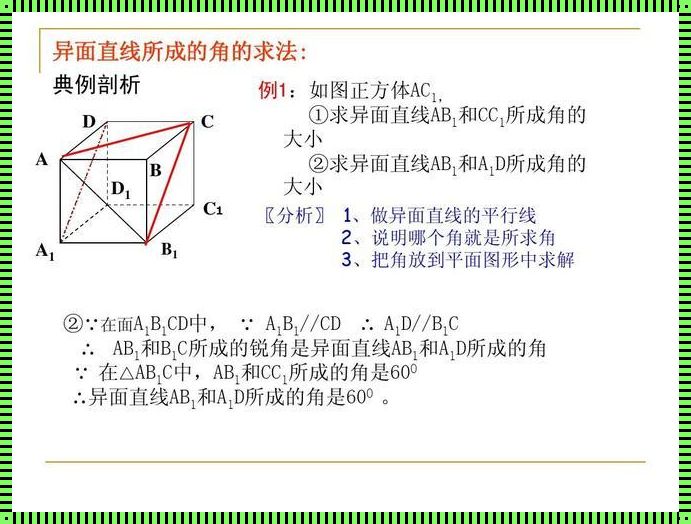
一、初识异面直线所求角

“异面直线”，顾名思义，就是不在同一个平面上的两条直线。那么，它们所形成的角该如何求解呢？别急，我们先来了解一下这个角的性质。

在三维空间中，两条异面直线所形成的角，其实就是一个平面角。这个角的大小，不会受到直线在空间中的位置影响，只与它们在平面上的投影有关。明白了这个性质，我们就可以开始寻找解题的突破口。

二、寻找解题的“金钥匙”

1. 画图表示

解决异面直线所求角的问题，首先需要将题目中的信息用图形表示出来。这里有一个小技巧，就是尽量将异面直线画在三维坐标系中，这样有助于我们更直观地观察它们的位置关系。

2. 寻找辅助线

在求解过程中，辅助线的运用至关重要。辅助线可以帮助我们找到异面直线在平面上的投影，从而构建出所需的角。那么，如何寻找辅助线呢？

（1）过直线外一点，作已知直线的平行线。

（2）过直线外一点，作已知直线的垂线。

（3）利用已知角度或长度关系，作相应角度或长度的线段。

3. 运用三角函数

在找到异面直线在平面上的投影后，我们可以利用三角函数求解所求角。这里需要注意的是，要熟练掌握正弦、余弦、正切等三角函数的定义和性质，才能在解题过程中游刃有余。

三、实战演练

下面，我们就通过一个具体的例子，来实战演练一下异面直线所求角的解题过程。

例题：已知空间直角坐标系中，直线L1：x=0，直线L2：y=0，直线L3：z=2，求直线L1与L3所形成的角。

解题步骤：

1. 画图表示：在三维坐标系中表示出三条直线。

2. 寻找辅助线：过点（0,0,2）作直线L1的平行线，交y轴于点A。

3. 构建平面角：连接点A和原点O，得到直线AO，即为异面直线L1与L3在平面上的投影。

4. 求解角度：利用三角函数，求解∠AOx。

四、总结与拓展

通过以上讲解，相信大家对异面直线所求角的解题方法已经有了深入的了解。其实，几何问题的解决往往离不开观察、联想和构造。在求解过程中，我们要善于运用已知信息，寻找解题的“金钥匙”。

此外，异面直线所求角问题还可以拓展到更广泛的领域，如空间向量、立体几何等。掌握了解题方法，我们就可以在几何学的世界中自由翱翔，探索更多未知的美景。

最后，希望这篇文章能让你在求解异面直线所求角问题时，不再感到困惑和无助。让我们一起，用智慧开启几何学的大门，领略其中的奥秘与乐趣吧！