在浩如烟海的综合资讯中，我们试图捕捉那最闪耀的星——显著性水平计算公式。今天，让我们一起揭开它神秘的面纱，探索其中的奥秘。

一、何为显著性水平计算公式？

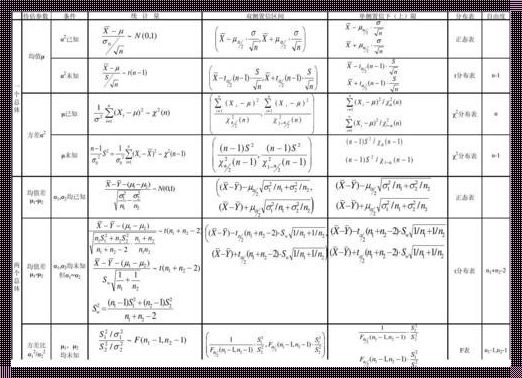
在研究现象、分析问题时，我们常常需要进行假设检验。而显著性水平计算公式便是这一过程中的关键所在。它帮助我们判断样本数据是否具有统计学意义，从而为我们的决策提供依据。那么，这个神秘的公式究竟包含哪些要素呢？

• 原假设（H0）与备择假设（H1）
• 检验统计量
• 显著性水平（α）
• p值

二、显著性水平计算公式背后的故事

你是否曾想过，为什么我们要设定一个显著性水平呢？这背后隐藏着一个有趣的故事。在统计学的早期，研究人员发现，当样本量固定时，假设检验的结果具有一定的概率性。这意味着，有时候我们会错误地拒绝一个正确的原假设，或者错误地接受一个错误的原假设。为了控制这种错误发生的概率，显著性水平应运而生。

那么，如何设定显著性水平呢？一般来说，显著性水平取0.05或0.01。这意味着，当我们拒绝原假设时，有5%或1%的几率犯第一类错误（错误地拒绝正确的原假设）。当然，这并不意味着显著性水平越低越好，我们需要在控制错误率与统计功效之间寻找平衡。

三、显著性水平计算公式在实际应用中的魅力

了解了显著性水平计算公式的基本概念，我们来看看它在实际应用中的魅力。以下三个案例，或许能让你对这个神秘公式有更深刻的认识。

1. 医学研究：假设检验在医学研究中具有重要意义。例如，研究人员可以通过假设检验来判断某种新药是否具有治疗效果。通过显著性水平计算公式，我们可以得出结论：在给定显著性水平下，新药是否具有统计学意义上的疗效。
2. 经济学研究：在经济学领域，假设检验同样发挥着重要作用。以需求曲线为例，我们可以通过显著性水平计算公式来判断价格与需求量之间的关系是否显著。
3. 心理学研究：在心理学领域，显著性水平计算公式可以帮助研究人员判断实验结果是否具有统计学意义。例如，通过假设检验，我们可以判断某种心理干预方法是否对改善焦虑症状具有显著效果。

四、结语

显著性水平计算公式，这个神秘的存在，贯穿于我们的研究、工作与生活。它帮助我们识别规律、发现现象，为我们的决策提供有力支持。然而，正如世上没有绝对的真理，我们需要理性地看待这个公式，避免陷入追求统计学意义的陷阱。

在探索显著性水平计算公式的过程中，我们感受到了统计学的魅力。让我们继续在这条道路上前行，揭示更多未知的世界，为人类的发展贡献我们的智慧。