自古以来，人类一直在探索科技的奥秘。今天，让我们揭开离散数学的神秘面纱，一窥其自反性、对称性与传递性的独特魅力。

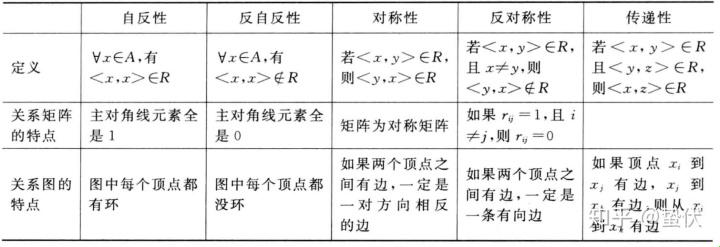
1. 离散数学：科技的基石

“离散数学，看似遥远，实则与我们息息相关。”这句话用来形容离散数学的地位再合适不过。那么，究竟什么是离散数学？简单来说，它是研究离散量的数学分支，如整数、图论等。在科技领域，离散数学发挥着举足轻重的作用。

2. 自反性：科技发展的内在动力

“自我反思，方能不断进步。”这句话同样适用于科技领域。自反性，即事物自身具备的一种自我关联特性。在科技发展过程中，自反性体现在科学家们对现有技术的不断质疑、改进和创新。

以人工智能为例，从最初的简单逻辑推理，到如今的深度学习、神经网络，无不是科学家们对现有技术自反性的体现。他们不断反思、优化算法，使人工智能得以飞速发展。

3. 对称性：科技之美

“对称之美，无处不在。”在科技领域，对称性同样具有重要意义。对称性，意味着事物在某种变换下保持不变。在离散数学中，对称性体现在图论、组合数学等方面。

以晶体学为例，晶体的对称性决定了其物理、化学性质。科学家们通过对称性原理，预测并发现了许多新型材料，为科技进步奠定了基础。

4. 传递性：科技发展的桥梁

“一石激起千层浪。”在科技领域，传递性起着串联各个领域、推动科技进步的作用。传递性，意味着事物之间的关联具有传递性。

以互联网为例，从计算机科学到通信技术，再到如今的人工智能、大数据，无不是在传递性作用下，各个领域相互促进、共同发展的结果。

5. 揭秘：离散数学的神奇魅力

“探索未知，是人类永恒的追求。”离散数学的自反性、对称性与传递性为我们揭示了科技发展的内在规律。那么，在实际应用中，这些特性又如何体现呢？

（1）计算机科学：从二进制到编程语言，再到操作系统，离散数学的自反性、对称性和传递性为计算机科学提供了理论基础。

（2）通信技术：在信息传输过程中，离散数学的对称性原理保证了信号传输的稳定性和可靠性。

（3）人工智能：深度学习、神经网络等技术的发展，离不开离散数学的支撑。自反性、对称性和传递性在算法优化、模型训练等方面发挥了重要作用。

6. 结语

“科技改变生活，离散数学引领未来。”今天，我们共同探讨了离散数学的自反性、对称性与传递性，领略了科技之奥秘。在未来，让我们继续探索未知，用智慧书写科技发展的新篇章。