偏序集与格，这可是数学里的老朋友了。今日，我就带着诸位边抱怨边探讨，究竟哪些偏序集拥有格的神奇魔力。

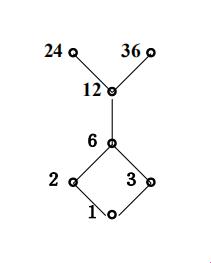
“你知道吗，偏序集就像是一群顽皮的孩子，有的规规矩矩，有的却调皮捣蛋。”旁边的某人一本正经地发表着高见。可不是嘛，格就是那些规规矩矩的孩子，让人省心。

在这个纷繁复杂的世界里，偏序集无处不在。从人际关系的网络，到计算机科学的数据结构，它们如影随形。然而，并非所有的偏序集都能享受到格的待遇。那么，哪些偏序集是格呢？

“让我猜猜，是不是那些有特殊癖好的偏序集？”某人调侃道。哈哈，癖好倒是没有，但特殊性质确实不少。

首先，你得有个“上确界”和“下确界”。这就好比是偏序集中的家长，管束着这群孩子，让他们不敢造次。有了这两个界限，偏序集才有了格的味道。

“哦，这么一说，我倒想起了那个著名的例子——实数集。”某人恍然大悟。

没错，实数集就是一个典型的格。它的上确界和下确界，让它在数学界独树一帜。然而，并非所有的偏序集都能像实数集一样风光。

“那是不是所有的偏序集都可以变成格呢？”某人好奇地问。

唉，如果真是这样，世界该有多美好。可惜，事实并非如此。有些偏序集，无论如何努力，都无法成为格。这就好比是那个无论如何都学不会数学的学生，让人头疼。

“比如说呢？”某人追问。

比如说，离散的整数集。它就偏偏不是格。你可能会抱怨，整数集这么规矩，怎么会不是格呢？可事实就是如此，它缺少那个至关重要的“上确界”和“下确界”。

“那有没有什么办法，让这些偏序集也变成格呢？”某人似乎对这个问题情有独钟。

办法嘛，自然是有的。有一种叫做“格的完备化”的技术，可以让一个偏序集摇身一变，成为格。这就像是给一个孩子请了个家庭教师，让他脱胎换骨。

“哇，这么神奇！”某人惊叹。

是啊，数学的世界就是如此奇妙。有时候，你可能会觉得它冷漠无情，难以捉摸。但当你深入了解，你会发现它其实充满了爱心和温暖。

“那我们是不是也可以把不是格的偏序集变成格呢？”某人满怀期待。

哈哈，如果真是这样，那我岂不是要失业了？可惜，并非所有的偏序集都能通过完备化成为格。有些偏序集，注定与格无缘。

“唉，真是无奈。”某人感慨。

可不是嘛，生活就是这样。有时候，我们会感到无助，甚至火爆。但别忘了，即使在这些不是格的偏序集中，也藏着许多美丽的秘密。

“那你说，我们该怎样去发现这些秘密呢？”某人若有所思。

那就需要我们用心去挖掘，用爱去感悟。在探讨偏序集与格的过程中，我们可能会遇到困难，甚至会抱怨。但请相信，只要我们持之以恒，总会有意想不到的收获。

“说得好！”某人拍手称赞。

最后，让我们回到最初的问题：哪些偏序集是格？现在，你或许已经有了答案。但更重要的是，我们在这个过程中，学会了抱怨，也学会了感悟。这，才是数学带给我们的最大财富。

偏序集与格，不过是一场游戏。而在这场游戏中，我们笑过、哭过，也成长了。这就是数学的魅力，让人又爱又恨。不是吗？