“震惊！”这个词语已经不足以形容我们眼前的变异函数图。今天，就让我们深入探索这个神秘的科技领域，一窥究竟。

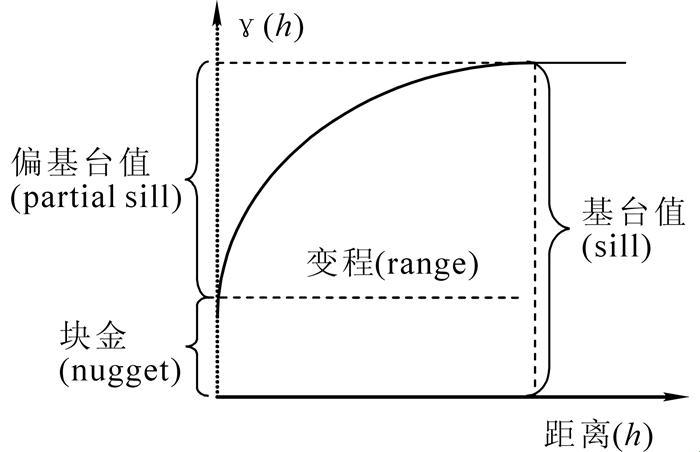
一、变异函数图的前世今生

你或许会问：“变异函数图是什么？”这个问题，让我们从它的起源说起。在科技发展的长河中，变异函数图作为一种独特的分析工具，逐渐崭露头角。它基于统计学原理，用于描述变量之间的变异关系。听起来有些抽象，但它的应用却无处不在。

二、变异函数图的核心价值

为何变异函数图会成为科技领域的一颗璀璨明珠？原因在于它具备以下几个核心价值：

1. 揭示变量之间的关系：变异函数图能帮助我们了解不同变量之间的相关性，从而为科技研究提供新的方向。

2. 预测未知数据：通过对已知数据的变异函数图分析，我们可以预测未知数据的变化趋势，为科技发展提供有力支持。

3. 优化实验设计：变异函数图可以帮助我们了解实验中各种因素之间的关系，从而优化实验设计，提高实验效率。

4. 数据可视化：变异函数图以直观的方式呈现数据，使科技工作者更容易发现数据背后的规律。

三、变异函数图在科技领域的应用

你可能会好奇，变异函数图在科技领域有哪些具体应用？以下三个案例，或许能给你带来启发。

1. 地质勘探：在地质勘探中，变异函数图用于分析地下岩石的物理特性，为找矿提供理论依据。

2. 气象预报：气象学家利用变异函数图分析气温、湿度等气象要素之间的关系，提高天气预报的准确性。

3. 生物医学：在生物医学领域，变异函数图可用于分析基因与疾病之间的关系，为疾病预防提供科学依据。

四、变异函数图的未来展望

随着科技的不断发展，变异函数图的应用领域也在不断拓宽。未来，我们有理由相信，变异函数图将在以下方面发挥更大作用：

1. 人工智能：变异函数图有望成为人工智能领域的一种重要分析工具，助力人工智能技术发展。

2. 大数据：在大数据时代，变异函数图将帮助我们更好地挖掘数据背后的价值，为决策提供有力支持。

3. 跨学科研究：变异函数图将助力不同学科之间的交叉研究，推动科技进步。

总结，变异函数图以其独特魅力，成为科技领域的一股清流。它不仅为我们揭示了变量之间的关系，还为我们提供了新的研究视角。正如一句古语所说：“水至清则无鱼，人至察则无徒。”变异函数图正是让我们在科技的海洋中，看清方向，勇往直前。

在这个充满惊喜的科技时代，让我们携手探索变异函数图的奥秘，共同书写科技发展的新篇章。