科技领域中，总有一些概念如同神秘的宝石，让人着迷。今天，让我们共同揭开行列式这枚宝石的神秘面纱，一探其几何性质背后的科技魅力。

一、何为行列式？

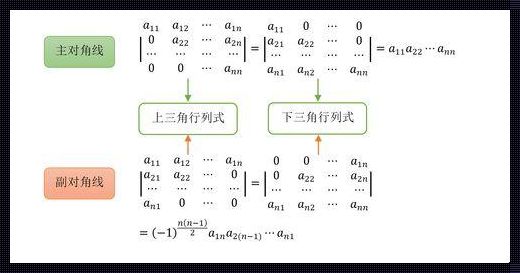
在我们开始探索行列式的几何性质之前，首先要明确什么是行列式。行列式，一个数学名词，看似与科技毫不相关，实则不然。它是线性代数中一个重要的概念，用以描述矩阵的某些特性。那么，它与几何性质有何关联呢？

事实上，行列式可以看作是空间中一个点、直线或平面变换后的“体积”。在二维空间中，它表示的是一个平行四边形的面积；而在三维空间中，它则代表一个四面体的体积。正是这种“体积”特性，使得行列式在几何性质的研究中具有重要意义。

二、行列式的几何性质

现在，让我们深入了解行列式的几何性质。以下三个性质，将带领我们踏入一个全新的科技世界。

• 性质一：行列式的值不变

  当一个矩阵经过一系列的行变换（如行交换、行相加或乘以常数）后，其行列式的值保持不变。这一性质为计算机图形学中的变换提供了理论基础，如投影变换、仿射变换等。

• 性质二：行列式的符号规律

  行列式的符号规律揭示了空间中点、直线或平面变换后的“方向”。例如，在二维空间中，行列式的正负表示两个向量构成的平行四边形在坐标平面上的位置关系。这一性质在计算机图形学中的光照计算、曲面渲染等方面具有重要意义。

• 性质三：行列式的行列式

  一个矩阵的行列式可以看作是一个新的矩阵，其元素为原矩阵各元素的代数余子式。这一性质使得行列式在求解线性方程组、矩阵求逆等方面具有广泛应用。

三、行列式与科技的不解之缘

那么，行列式在科技领域中的应用究竟如何呢？以下三个例子，将让我们见识到行列式的科技魅力。

• 实例一：计算机图形学

  在计算机图形学中，行列式被广泛应用于几何变换。通过对矩阵的行列式进行计算，我们可以得到变换后的图形在空间中的位置、方向和大小。这为图形渲染、动画制作等领域提供了便利。

• 实例二：机器人学

  在机器人学中，行列式同样发挥着重要作用。通过对机器人关节的变换矩阵进行行列式计算，我们可以得到机器人末端执行器的位置和姿态。这为机器人路径规划、运动控制等领域提供了理论基础。

• 实例三：物理学

  在物理学中，行列式被用于描述电磁场、量子力学等领域中的变换关系。例如，电磁场中的麦克斯韦方程组可以通过行列式的形式表示，从而为电磁波的传播、电磁场的计算等提供了简洁的数学工具。

四、结语

行列式，这个看似普通的数学概念，却在科技领域发挥着举足轻重的作用。其几何性质为我们揭示了空间变换的奥秘，为计算机图形学、机器人学、物理学等众多领域提供了理论基础。如今，我们已经揭开了行列式的神秘面纱，领略了其科技魅力。在未来，让我们继续探索这个神奇的世界，用行列式这把钥匙，开启更多的科技之门。