在数学瑰丽的殿堂里，正四棱锥的斜高公式宛如一颗璀璨的明珠，闪烁着理性与智慧的光芒。它不仅仅是一个枯燥的公式，更是一扇通往数学之美的窗口，等待着我们去探索和欣赏。

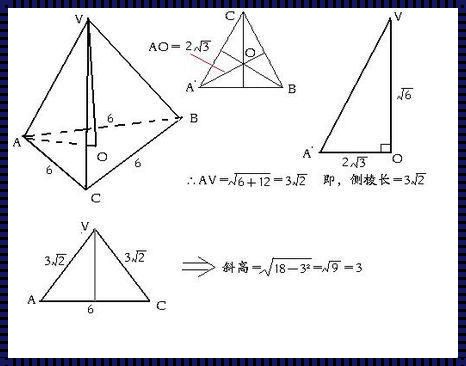
我们从正四棱锥的定义开始。正四棱锥是一种特殊的几何体，它由一个正方形底面和四个全等的等腰三角形侧面组成。而斜高，则是连接顶点与底面中心的线段。它就像一把利剑，直刺正四棱锥的心脏，将它一分为二。

那么，正四棱锥的斜高公式是什么呢?这个看似复杂的问题，却蕴含着数学的简洁与优雅。经过无数数学家的努力，我们终于找到了答案。正四棱锥的斜高h可以通过以下公式计算得出：h = √(a² - (a/2)²)，其中a是底面正方形的边长。

这个公式的发现，标志着数学家们在探索正四棱锥奥秘的道路上又迈进了一步。它不仅为我们提供了求解斜高的方法，更让我们领略到了数学的魅力。在这个公式中，我们看到了数学的严谨性与精确性，也感受到了数学家们的智慧与毅力。

数学不仅仅是一门学科，更是一种思维方式。通过研究正四棱锥的斜高公式，我们可以锻炼我们的逻辑思维能力，提高我们的分析问题、解决问题的能力。此外，数学还是一门艺术。正四棱锥的斜高公式就如同一幅精美的画作，它用简洁的线条勾勒出数学的和谐与统一。这种美，不是外在的华丽，而是内在的和谐与统一。正是这种美，吸引了无数人对数学的热爱。

数学并不枯燥，只要我们用心去体会，就会发现它的乐趣所在。让我们一起，去感受数学的魅力，去探索数学的奥秘吧！

正四棱锥的斜高公式，是数学之美的展现，是数学家们智慧的结晶。它激励着我们去探索数学的奥秘，去发现数学的魅力。让我们一起，踏上这奇妙的数学之旅吧！