在一个看似普通的数学问题中，我们惊现了一个神秘而有趣的现象——单个2×2矩阵计算的神奇魔力。这不禁让我们对这个看似简单的数学问题产生了浓厚的兴趣，一探究竟。

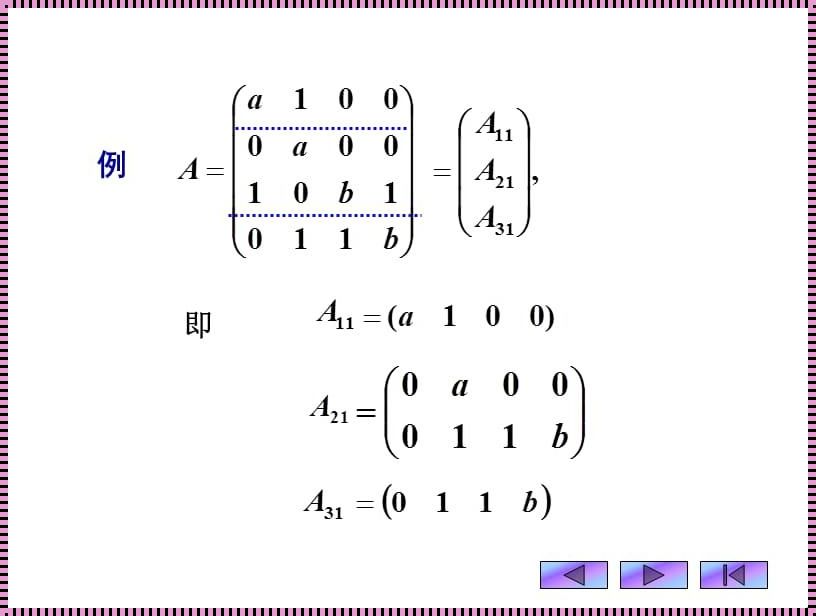
我们先来了解一下2×2矩阵。一个2×2矩阵是这样的：

\[

\begin{pmatrix}

a & b \\

c & d

\end{pmatrix}

\]

其中，a、b、c、d都是实数。这个矩阵可以表示一个线性变换，将一个二维向量转换为另一个二维向量。这个变换是如何进行的呢？其实，这个过程就是矩阵乘法。

假设我们有一个二维向量 \(\begin{pmatrix}x \\ y\end{pmatrix}\)，我们将这个向量与2×2矩阵 \(\begin{pmatrix}a & b \\ c & d\end{pmatrix}\)相乘，得到的结果是另一个二维向量 \(\begin{pmatrix}ax + by \\ cx + dy\end{pmatrix}\)。这个过程就是线性变换。

那么，单个2×2矩阵计算的神奇魔力在哪里呢？其实，就在于这个矩阵的四个元素——a、b、c、d。这四个元素的不同组合会产生不同的线性变换，从而产生各种有趣的现象。

例如，当a和d都是正数时，这个矩阵表示的是一个拉伸变换，将向量沿着x轴和y轴方向拉伸；当a和d都是负数时，这个矩阵表示的是一个压缩变换，将向量沿着x轴和y轴方向压缩；当a和d一正一负时，这个矩阵表示的是一个旋转变换，将向量旋转一个角度。

更神奇的是，当a、b、c、d满足一定的条件时，这个矩阵还可以表示一些特殊的变换，比如镜像变换、错切变换等。这些变换在计算机图形学、物理学、工程学等领域有着广泛的应用。

总的来说，单个2×2矩阵计算的神奇魔力在于其可以表示各种线性变换，从而产生各种有趣的现象。这让我们对这个看似简单的数学问题产生了浓厚的兴趣，也让我们对数学的奥秘有了更深的认识。