在数学的广袤宇宙中，哈斯图（Hasse diagram）是一副描绘偏序集（partial order）关系的直观工具。在这副图中，我们如何去辨别那些至高无上和至低无下的元素——极大元（maximal elements）与极小元（minimal elements）呢？

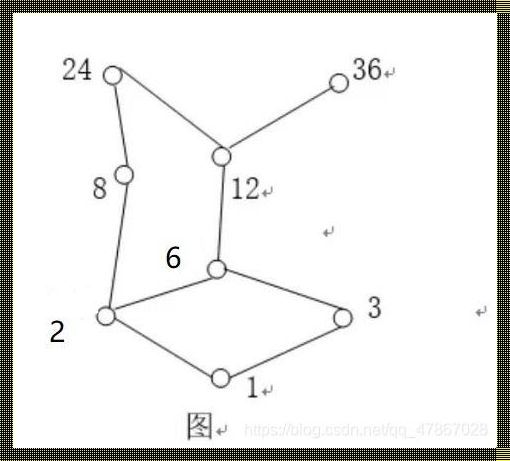
首先，让我们先明确几个概念。在一个偏序集中，如果一个元素x大于或等于集内所有其他元素，那么我们称x为偏序集中的极大元。换句话说，极大元是没有比它更高的元素了。同理，如果一个元素y小于或等于集内所有其他元素，那么y就是偏序集中的极小元，意味着没有比它更低的元素了。

在哈斯图的框架下，极大元通常位于图的顶层，而极小元则位于底层。这是因为在图中，如果两个元素之间存在一条直接或间接的路径，那么我们称这两个元素在偏序集中是相互关联的。极大元不关联任何其他元素，因为没有任何元素能超越它们，而极小元也不关联任何其他元素，因为没有任何元素能低于它们。

为了更好地理解这一概念，我们可以借助一个简单的例子：考虑一个由数字组成的集合，这个集合的偏序关系是基于这些数字的大小。在这个集合中，数字10是一个极大元，因为没有其他数字比10更大；而数字0是一个极小元，因为没有其他数字比0更小。在哈斯图中，10将位于顶层，而0将位于底层。

但事情并非总是这么简单。在某些情况下，一个偏序集可能没有极大元或极小元。比如说，如果我们考虑由所有正整数组成的集合，并定义它们之间的偏序关系为“大于等于”，那么这个集合就没有极大元，因为总有更大的数存在。同样地，如果考虑由所有非负整数组成的集合，并定义它们之间的偏序关系为“小于等于”，那么这个集合就没有极小元。

通过哈斯图，我们可以对这些概念有更直观的理解。在图中，元素之间的直接关系用线段表示，无直接关系的则意味着在偏序集中存在不可达性。极大元和极小元的存在与否，取决于集合和偏序关系的具体性质。

在研究极大元和极小元的过程中，我们不仅学习到了数学中关于大小比较和排序的知识，同时也深入探讨了逻辑和算术的交汇点。每一个极大元和极小元的发现，都像是在数学的迷宫中点亮了一盏明灯，指引我们走向真理的彼岸。