当我们谈到F检验时，我们通常是在讨论统计学中的一个重要概念。F检验是一种用于比较两个或多个样本、群体平均值是否存在显著差异的统计方法。在F检验中，我们通常会关注一个特定的数字——F统计量。这个数字对于我们得出结论至关重要，因为它可以帮助我们判断样本数据是否支持我们的假设。

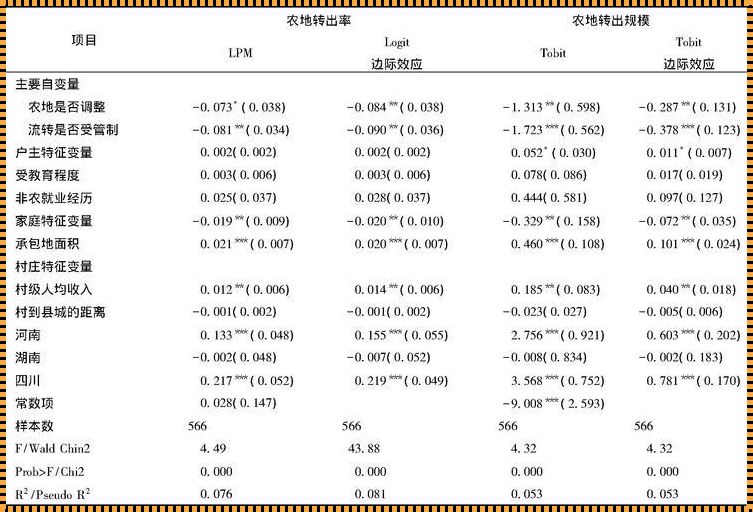
在F检验中，我们通常会关注两个重要的数字：第一是自由度，第二是概率值。自由度是统计学中一个重要的概念，它代表了我们可以自由变动的独立变量数量。概率值则代表了我们得出特定结果的可能性。这两个数字对于我们解释F统计量至关重要。

当我们进行F检验时，我们会得到一个F统计量的值。如果这个值大于临界值，我们就拒绝原假设，认为样本数据支持我们的备择假设。反之，如果我们得到的F统计量小于临界值，我们就接受原假设，认为样本数据不支持我们的备择假设。

然而，F检验并不仅仅是一个简单的计算过程。它背后蕴含着深奥的统计学原理。F检验的本质是比较两个样本、群体平均值的标准差。如果我们认为两个样本、群体平均值的标准差存在显著差异，那么我们就可以认为这两个样本、群体平均值本身也存在显著差异。

在现实生活中，F检验的应用非常广泛。它可以用于教育领域，帮助我们判断不同教学方法对学生成绩的影响；它可以用于医学领域，帮助我们判断不同治疗方法对患者疗效的差异；它还可以用于社会科学领域，帮助我们分析社会现象背后的原因。

然而，尽管F检验在统计学中具有重要地位，我们也要注意到它的局限性。F检验的结果受到样本数据的影响，如果样本数据存在偏差，那么F检验的结果也可能不准确。因此，在实际应用中，我们需要结合其他统计方法，全面分析样本数据，以得出更为可靠的结论。

总之，F检验括号后面的两个数字——自由度和概率值，对于我们理解和解释F统计量至关重要。它们帮助我们判断样本数据是否支持我们的假设，从而揭示样本数据背后的深层含义。然而，我们也要注意到F检验的局限性，在实际应用中，需要结合其他统计方法，全面分析样本数据。通过这种方式，我们才能更好地运用F检验，探索统计学中的奥秘。