在数学和科学领域，创建坐标系是进行定量分析和描述现象的基础。坐标系为我们提供了一种在二维或三维空间中定位和表示点、线、面和体的方式。本文将深入探讨创建坐标系的五种方法，以揭开其神秘面纱。

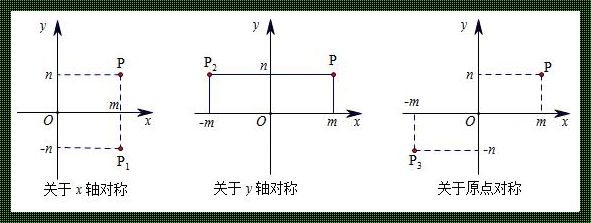
首先，笛卡尔坐标系是最为常见的坐标系，由法国哲学家勒内·笛卡尔引入。它由两条互相垂直的数轴组成，通常表示为x轴和y轴。这种坐标系在平面几何和直线方程中起着关键作用，使我们能够轻松地解决各种几何和代数问题。

其次，极坐标系是基于角度和距离的坐标系，由德国数学家卡尔·弗里德里希·高斯推广。在极坐标系中，一个点的位置可以用一个角度（通常称为极角）和一个距离（通常称为极径）来描述。极坐标系在处理圆形和旋转物体时非常有用，因为它简化了对角度和距离的运算。

第三，柱坐标系（或圆柱坐标系）是由德国数学家莱昂哈德·欧拉提出的。它由两个互相垂直的数轴组成，一个表示高度，另一个表示圆周上的角度。柱坐标系在描述具有圆形对称性的物体时非常有用，如圆柱和球体。

第四，球坐标系是由俄国数学家尼古拉·罗巴切夫斯基引入的。它基于三个互相垂直的数轴，分别表示球面上的角度和两个垂直方向的距离。球坐标系在处理球体和旋转对称的物体时非常有用，因为它能够更直观地描述物体在三维空间中的位置。

最后，复平面坐标系是由德国数学家卡尔·魏尔斯特拉斯提出的。它由实数轴和虚数轴组成，用于表示复数。复平面坐标系在复数和复变函数的研究中起着关键作用，为我们提供了一种可视化复数和复平面上的点的方法。

总之，创建坐标系是数学和科学领域中不可或缺的工具。通过了解和掌握五种主要的坐标系，我们可以更好地描述和分析各种几何和物理现象。无论是解决简单的代数问题，还是研究复杂的物理现象，坐标系都为我们提供了一种强大的工具，帮助我们揭开世界的神秘面纱。