在数学的世界里，平面直角坐标系是一种基础而重要的工具，它能够帮助我们准确地描述和分析现实世界中的点、线、面等几何对象。而平面直角坐标系的建立，背后有着严谨的原则和深刻的数学思想。

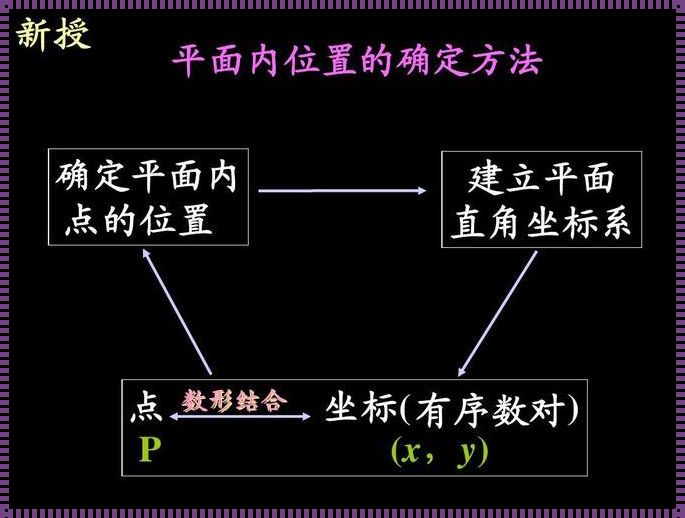
首先，平面直角坐标系的建立依赖于两条互相垂直的数轴，即横轴和纵轴。这两条数轴分别代表着实数集中的水平和垂直方向，它们的交点被称为原点。这种建立方式，既简洁又直观，能够让我们清晰地认识到几何对象与实数集之间的关系。

其次，平面直角坐标系建立的原则还包括了坐标轴的无限延伸。这意味着，无论我们选择哪个点作为观察对象，都可以在其对应的坐标轴上找到一个与之对应的唯一实数。这种一一对应的关系，使得我们能够用精确的数学语言来描述和分析几何对象。

此外，平面直角坐标系的建立还遵循了对称性和一致性的原则。对称性体现在坐标系的任意一条轴都是对称的，即对于任意一个点，其在坐标系中的位置与其关于原点的对称点的位置是对称的。一致性则体现在坐标系的每个轴都是均匀的，即坐标轴上的每个单位长度代表的实数值是相同的。

通过这些原则的建立，平面直角坐标系不仅为我们提供了一种精确描述几何对象的工具，还让我们深入地理解了数学中的逻辑思维和方法。我们可以通过坐标系来研究函数的图像、分析线性方程组的解、探讨两点之间的距离和角度等，这些都是平面直角坐标系带来的便利。

然而，平面直角坐标系的建立并非一蹴而就，它是数学家们长时间思考和探索的结果。从古希腊时期的几何学，到17世纪的笛卡尔坐标系，再到现代数学的发展，平面直角坐标系不断地被完善和优化。这个过程，不仅是数学知识的积累，更是数学思想的发展。

总之，平面直角坐标系的建立原则不仅揭示了数学的严谨性和逻辑性，也让我们看到了数学的美丽和力量。它是我们探索数学世界的基础，也是我们理解现实世界的工具。让我们用心去感受这个坐标系的奥秘，用它来打开数学的大门，探寻更多的知识宝藏。