几何世界中，四棱锥这个立体图形的独特性质引发了一个有趣的问题：它是否一定有内切球？这个问题在数学领域中引起了广泛的讨论。今天，让我们一起揭开这个问题的神秘面纱，探索四棱锥与内切球之间的奥秘。

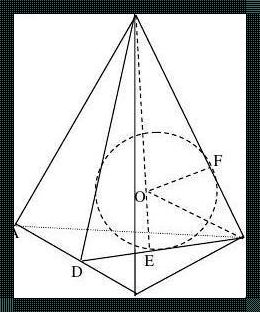
首先，让我们回顾一下四棱锥的基本性质。四棱锥是一个有四个侧面和一个底面的立体图形，底面是一个四边形，侧面是四个三角形。它的顶点是底面的一个顶点，而底面的其他三个顶点以及侧面与底面的交点构成了四棱锥的四个侧顶点。

内切球是指在一个立体图形内部，能够与图形的每一个面相切的球体。那么，四棱锥是否一定有内切球呢？答案是否定的。事实上，只有当四棱锥的形状满足特定条件时，才存在内切球。

让我们通过一个生动的例子来理解这个概念。想象一个正四棱锥，底面是一个正方形，侧面是四个等边三角形。这个四棱锥的形状非常特殊，它的侧面和底面都是正多边形，且侧面的边长等于底面的边长。在这种情况下，我们可以找到一个内切球，它的半径与四棱锥的高相等。这个内切球能够与四棱锥的每一个面相切，形成一个完美的切面。

然而，对于一般的四棱锥，即底面和侧面不一定是正多边形的情况，内切球的存在并不 guaranteed。这是因为四棱锥的侧面和底面之间的角度关系可能不满足内切球的切面条件。在非特殊的四棱锥中，我们无法找到一个球体，使其能够与四棱锥的每一个面都相切。

通过这个探索，我们深入了解了四棱锥和内切球之间的关系。虽然并非所有的四棱锥都拥有内切球，但特殊形状的四棱锥确实存在内切球。这个发现不仅增加了我们对几何图形的理解，也激发了我们对数学奥秘的探索欲望。

四棱锥和内切球的关系不仅仅是一个数学问题，它还涉及到物理学和工程学等领域。例如，在计算四棱锥的体积或表面积时，内切球的存在可以提供一种简化的方法。此外，内切球的概念在研究多面体的结构性质和优化问题中也具有重要意义。

总结起来，四棱锥是否一定有内切球这个问题揭示了数学世界中的一个有趣现象。通过深入探索四棱锥和内切球之间的关系，我们不仅增加了对几何图形的理解，也激发了对数学奥秘的探索欲望。四棱锥和内切球的关系将继续在数学、物理学和工程学等领域发挥重要作用，引领我们进一步发现和创造。